MarkTheQuark
- 5
- 2
I'm stuck in a problem of a spring mass system with a pendulum attached to it as showed in the figure below:
My goal is to find the movement equation for the mass, using Lagrangian dynamics.
If the spring moves, the wire will move the same amount. Therefore, we can write the x and y position of the mass in terms of this displacement, the length of the wire, and the theta angle.
The problem I'm having is getting to identify the potential energy of the spring, using these terms so that when solving the LaGrange equation it gives a restoring force term of the spring.
Can anyone help me identifying this?
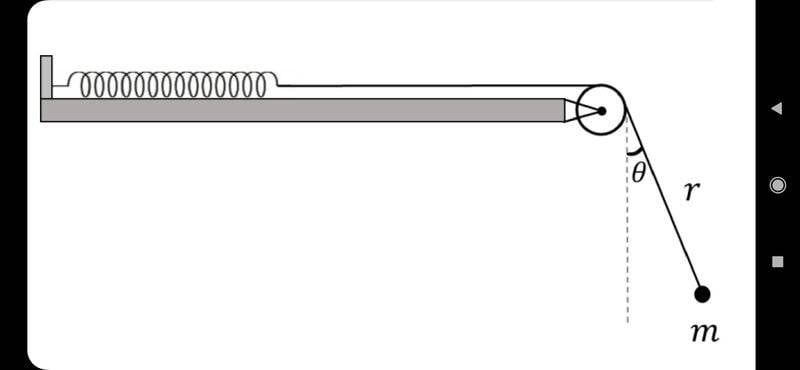
My goal is to find the movement equation for the mass, using Lagrangian dynamics.
If the spring moves, the wire will move the same amount. Therefore, we can write the x and y position of the mass in terms of this displacement, the length of the wire, and the theta angle.
The problem I'm having is getting to identify the potential energy of the spring, using these terms so that when solving the LaGrange equation it gives a restoring force term of the spring.
Can anyone help me identifying this?