SR Doppler Effect: Differences in Wave VS Momentum Models

[tade]

...We can form the vector $\vec{E} \times \vec{B}$ and show that it is a 3-vector $\vec{p}$ with an associated energy $E$ that satisfies the classical massless particle relation above.

In that same paper, Einstein derived an expression for relativistic KE, which has been applied to classical massless particles.

We will now determine the kinetic energy of the electron. If an electron moves from rest at the origin of co-ordinates of the system K along the axis of X under the action of an electrostatic force X, it is clear that the energy withdrawn from the electrostatic field has the value

. As the electron is to be slowly accelerated, and consequently may not give off any energy in the form of radiation, the energy withdrawn from the electrostatic field must be put down as equal to the energy of motion W of the electron. Bearing in mind that during the whole process of motion which we are considering, the first of the equations (A) applies, we therefore obtain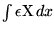

Einstein did this by using the E and B field transformations:

He plugged these transformations into the Lorentz force law in order to determine how a force transforms between frames.

From that he was able to derive an expression for KE.How might this derivation be modified in order to accurately account for the Doppler shifts of spherical wavefronts instead of just plane waves?

 

[Dale]

Einstein did this by using the E and B field transformations:
...
How might this derivation be modified in order to accurately account for the Doppler shifts of spherical wavefronts instead of just plane waves?

Probably start with the E and B field for your spherical wavefront and transform those instead. Maybe the standard dipole field wold be best. The math would get annoying pretty fast.

 

[tade]

Probably start with the E and B field for your spherical wavefront and transform those instead. Maybe the standard dipole field wold be best.

Do these apply to spherical wavefronts?

 

[Dale]

Do these apply to spherical wavefronts?

Not as written since the fields are written only as functions of x. I would construct the EM tensor and use that instead.

 

[tade]

Not as written since the fields are written only as functions of x. I would construct the EM tensor and use that instead.

oh f***, I'm so dumb.

https://en.wikipedia.org/wiki/Class...rmation_of_the_fields_between_inertial_frames

I thought that the transformations applied to all points in space, and the Wikipedia article didn't make it clear that it was only for x.

 

[Justintruth]

...model uses spherical Doppler wavefronts, why is this model inaccurate?

I don't know if its relevant to your problem but spherical wavefronts are impossible. To see why imagine the E or B vectors on a sphere. The Euler characteristic of a sphere is 2. Roughly the Euler characteristic can be seen to represent the minimum number of places where the wind speed must be zero. So if you imagine wind blowing on a sphere you will always have at least two places where the wind does not blow. On a torus you can have zero as the wind can blow up through the center around down and back in and up. The Euler characteristic is 0 for a Torus. So that means the curl of any vector field on a sphere must be 0 in at least two places. The E and B fields therefore must be zero. in fact this is true and all so called omni antennas have nulls.

 

[tade]

I don't know if its relevant to your problem but spherical wavefronts are impossible. To see why imagine the E or B vectors on a sphere. The Euler characteristic of a sphere is 2. Roughly the Euler characteristic can be seen to represent the minimum number of places where the wind speed must be zero. So if you imagine wind blowing on a sphere you will always have at least two places where the wind does not blow. On a torus you can have zero as the wind can blow up through the center around down and back in and up. The Euler characteristic is 0 for a Torus. So that means the curl of any vector field on a sphere must be 0 in at least two places. The E and B fields therefore must be zero. in fact this is true and all so called omni antennas have nulls.

I see, but I don't think it is that relevant.

What I said in #35, is it correct?