SR Doppler Effect: Differences in Wave VS Momentum Models

[tade]

In his seminal paper on Special Relativity: On the Electrodynamics of Moving Bodies, Einstein derives a formula for the Relativistic Doppler effect.

See this section:
§ 7. Theory of Doppler's Principle and of AberrationThe formula is:

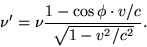In this Wiki article, the same formula is derived.
The article uses the "the standard Lorentz transformation of the four-momentum".

Now here's where it gets a little muddling.

Einstein writes:

In the system K, very far from the origin of co-ordinates, let there be a source of electrodynamic waves, which in a part of space containing the origin of co-ordinates may be represented to a sufficient degree of approximation by the equations

...if an observer is moving with velocity v relatively to an infinitely distant source of light...

It seems that his formula is a good approximation when we are sufficiently far from the source.

However, the four-momentum transformations do not depend on distance, yet they arrive at the exact same formula.

What's the reason for this difference?

 

[robphy]

I think this is he is using the approximation of a plane wave (for simplicity).

 

[tade]

I think this is he is using the approximation of a plane wave (for simplicity).

The four-momentum transformations are exact and don't depend on distance, so the formula derived from them should be considered exact. Why would it be identical to Einstein's formula if Einstein's formula was just an approximation?

 

[Dale]

Because Einstein's formula approximates the exact formula in the case where the approximation is valid.

 

[tade]

Because Einstein's formula approximates the exact formula in the case where the approximation is valid.

No, actually the formula printed in Einstein's paper is identical to the exact formula and it is a far-field approximation of another formula.
But semantics aside, I get what you mean.

However, this indicates that Einstein's Doppler model is inaccurate. Einstein's model uses spherical Doppler wavefronts, why is this model inaccurate?

 

[Dale]

Einstein's model uses spherical Doppler wavefronts, why is this model inaccurate?

The model is fine, but his equations are for a plane wave. So his equations don't match the model, except in the approximation he describes.

 

[tade]

The model is fine, but his equations are for a plane wave. So his equations don't match the model, except in the approximation he describes.

I understand that he uses plane waves since this is the far-field approximation.

But, if Einstein took all the spherical wavefronts into account and came up with an exact formula based upon that, that formula would differ from the printed formula, which means it would differ from the formula derived from the four-momentum transformations.

So if we consider the Doppler model exact, or if we consider the four-momenta exact, we arrive at different results. Which should not be. Maybe there's a catch somewhere, but I don't know where it could lie.

 

[PAllen]

The 4 momentum is for a 'particle of light'. That is, the geometric optics approximation. It is exact for a classical massless particle, and not exact for classical EM radiation.

 

[Dale]

I understand that he uses plane waves since this is the far-field approximation.

Then I don't understand your question. If you understand that he is approximating a spherical wave as a plane wave then what are you confused about? With that approximation Wikipedia and Einstein match.

But, if Einstein took all the spherical wavefronts into account

But he didn't, so this supposition it isn't relevant.

So if we consider the Doppler model exact, or if we consider the four-momenta exact, we arrive at different results.

The spherical Doppler is approximately a plane wave (per Einstein's approximation), which is exactly the four momentum.

 

[tade]

The 4 momentum is for a 'particle of light'. That is, the geometric optics approximation. It is exact for a classical massless particle, and not exact for classical EM radiation.

Ok I see it now.

Is there a 4-momentum-esque formula that is exact for classical EM radiation?

 

[tade]

With that approximation Wikipedia and Einstein match.

Lol, and that's the entire crux of my question.

But he didn't, so this supposition it isn't relevant.

Why is it irrelevant just because he didn't try that in his paper? It is relevant to the question I'm asking.

The spherical Doppler is approximately a plane wave (per Einstein's approximation), which is exactly the four momentum.

Is that the same as what PAllen has said? If that's the case then:

Is there a 4-momentum-esque formula that is exact for classical EM radiation?

If you think I sound churlish or truculent, I can assure you that that's not my intention, though I may sometimes inadvertently come across as so.

 

[PeterDonis]

Is there a 4-momentum-esque formula that is exact for classical EM radiation?

No. You can't describe classical EM radiation with a 4-vector. You need an antisymmetric 2-index tensor.

 

[tade]

No. You can't describe classical EM radiation with a 4-vector. You need an antisymmetric 2-index tensor.

PAllen mentioned "classical massless particle".

Does this mean that the further we are from the Doppler source, the more the EM radiation behaves like classical massless particles, and the closer the 2-index tensor approximates the 4-vector?

 

[SiennaTheGr8]

It might help to focus on the angle in that formula. And I think Einstein's wording leaves something to be desired about what the angle represents.

Here's how I'd put it:

A source emits an idealized unidirectional light wave. Think of it as a laser pulse or a photon if you'd like, or as a wave front sufficiently far away from the source to be regarded as unidirectional (that's what Einstein is getting at). In the source's rest frame, the light wave has frequency $f$. Now consider an observer moving with some arbitrary constant velocity $\vec \beta = \vec v / c$ relative to the source. Say that $\vec \beta$ forms an angle $\theta$ with the direction of propagation of the emitted light wave (as measured in the source's rest frame). Einstein's Doppler formula tells us that in the moving observer's rest frame, the light wave has frequency

$f^\prime = \gamma \left( 1 - \beta \cos \theta \right) f$,

where $\beta = |\vec \beta|$ and $\gamma = (1 - \beta^2)^{-1/2}$. Also note that $\beta \cos \theta$ is simply the component of $\vec \beta$ that's parallel to the direction of propagation of the light wave (as measured in the source's rest frame).

If the light wave were spherical, the formula would still work, but the $\theta$ would need to be updated for each "part" of the wave.

Does that help at all?

 

[PeterDonis]

PAllen mentioned "classical massless particle".

Does this mean that the further we are from the Doppler source, the more the EM radiation behaves like classical massless particles, and the closer the 2-index tensor approximates the 4-vector?

No. It only means that for one particular purpose, calculating the Doppler shift of the radiation, using a 4-vector is a good enough approximation far away from the source. There are still aspects of the radiation that are not captured in this approximation, and which can be probed by other measurements besides those that measure the Doppler shift. (For example, you can't explain the signal that comes through your radio antenna by describing the incoming radiation as a 4-vector, even if you are far away from the source.)

 

[tade]

It might help to focus on the angle in that formula. And I think Einstein's wording leaves something to be desired about what the angle represents.

Here's how I'd put it:

A source emits an idealized unidirectional light wave. Think of it as a laser pulse or a photon if you'd like, or as a wave front sufficiently far away from the source to be regarded as unidirectional (that's what Einstein is getting at). In the source's rest frame, the light wave has frequency $f$. Now consider an observer moving with some arbitrary constant velocity $\vec \beta = \vec v / c$ relative to the source. Say that $\vec \beta$ forms an angle $\theta$ with the direction of propagation of the emitted light wave (as measured in the source's rest frame). Einstein's Doppler formula tells us that in the moving observer's rest frame, the light wave has frequency

$f^\prime = \gamma \left( 1 - \beta \cos \theta \right) f$,

where $\beta = |\vec \beta|$ and $\gamma = (1 - \beta^2)^{-1/2}$. Also note that $\beta \cos \theta$ is simply the component of $\vec \beta$ that's parallel to the direction of propagation of the light wave (as measured in the source's rest frame).

If the light wave were spherical, the formula would still work, but the $\theta$ would need to be updated for each "part" of the wave.

Does that help at all?

Not really. Because my question is also about the energy momentum 4-vectors. Thanks for this anyway.

 

[SiennaTheGr8]

Hm.

Doesn't the four-momentum derivation get us precisely the same formula, with the same domain of applicability?

So we start with the general four-momentum:

$\vec P = (E, \vec p c)$.

Since it's a four-vector, its components obey the Lorentz transformation. Specifically (with standard configuration):

$E^\prime = \gamma(E - \beta \, p_x c)$.

Too lazy to do the trigonometry right now (maybe someone else will?), so let's just simplify this and say that all the momentum is in the x-direction: $p = p_x$. Now the Lorentz transformation for energy can be written:

$E^\prime = \gamma(E - \beta \, pc)$.

For our idealized unidirectional monochromatic light wave, classical EM gives us $E = pc$. So:

$E^\prime = \gamma(E - \beta E) = \gamma (1 - \beta) E$

And classical EM also tells us that frequency and energy are proportional. Thus:

$f^\prime = \gamma \left( 1 - \beta \right) f$,

which is Einstein's Doppler shift for $\theta = 0$. If we didn't simplify things with $p = p_x$, we'd get the $\cos \theta$ in there, yes?

 

[PeterDonis]

Doesn't the four-momentum derivation get us precisely the same formula, with the same domain of applicability?

Yes. But that domain of applicability is limited; it does not capture all of the properties of EM radiation, as I pointed out in a previous post.

 

[Dale]

Why is it irrelevant just because he didn't try that in his paper?

It is irrelevant because his equations and claims are for plane waves, not spherical waves, and the Wikipedia derivation is also for plane waves. Spherical waves are not considered in either source, so they are not relevant to the comparison of the two sources. It is like reading two travel books on Singapore, getting confused, and then trying to resolve it by asking a question about Hong Kong. Yes, your plane may have flown through Hong Kong to get Singapore, but once there you expect every book to show the same streets.

The four momentum is for a plane wave. Einstein points out that the field far from a source is approximately a plane wave. Einstein uses the plane wave approximation to derive a formula for plane waves which is identical to the plane wave formula used by Wikipedia in another way. Then you are surprised by the fact that the Einstein plane wave equation matches the Wikipedia plane wave equation. This should not be surprising.

 

[vanhees71]

Here seems to be a lot of unnecessary confusion. Of course, electrodynamics can be written in manifest covariant form. It's a Poincare invariant local classical field theory and as such can be formulated with Minkowski tensors (I restrict myself to special relativity here). To see this, we start with the usual non-covariant formalism (although it can be made also covariant, using the Silberstein-vector representation, but that's an advanced topic) 1+3-D formalism in a fixed inertial reference. I use Heaviside-Lorentz units, which are the most convenient and natural ones in the context of relativistic electromagnetics. The homogeneous Maxwell equations read
$$\vec{\nabla} \cdot \vec{B}=0, \quad \vec{\nabla} \times \vec{E}+\frac{1}{c} \partial_t \vec{B}=0.$$
From the first equation we see that (at least locally) there exists a vector potential, $\vec{A}$ such that
$$\vec{B}=\vec{\nabla} \times \vec{A}.$$
Plugging this in the 2nd equation gives
$$\vec{\nabla} \times \left ( \vec{E}+\frac{1}{c} \partial_t \vec{A} \right)=0,$$
and thus the field in the parenthesis is (at least locally) a gradient field
$$\vec{E}=-\vec{\nabla} A^0 - \frac{1}{c} \partial_t \vec{A}.$$
Now I've already written $A^0$ for the scalar potential, which is suggestive for putting $(A^0,\vec{A})$ together as components of a Minkowski four-vector field, $A^{\mu}$. Now we have to check whether the inhomogeneous Maxwell equations are compatible with that.

We first note that the charge density and current density can be put into a four-vector field,
$$(j^{\mu})=(c \rho,\vec{j}).$$
Indeed we can write for a charged-particle flow $\vec{v}$,
$$(j^{\mu})= \rho (c,\vec{v})=\frac{\rho}{\gamma} c (\gamma,\gamma \vec{\beta})=\rho_0 c (u^{\mu}),$$
where
$$\vec{\beta}=\frac{\vec{v}}{c}, \quad \gamma=\frac{1}{\sqrt{1-\vec{\beta}^2}}.$$
Now $\rho_0$ is the density in the (local) restframe of the fluid cell and as such a scalar, while the four-velocity
$$(u^{\mu})=\gamma (1,\vec{\beta})$$
is a four-vector field, and thus $(j^{\mu})$ is indeed a four-vector field.

Now let's see what the inhomogeneous Maxwell equations tell. In (1+3) form they read
$$\vec{\nabla} \cdot \vec{E}=\rho=\frac{1}{c} j^0, \quad -\frac{1}{c} \partial_t \vec{E}+\vec{\nabla} \times \vec{B}=\frac{1}{c} \vec{j}.$$
To see that these are in fact Poincare-covariant equations, we plug in the potentials and use $x^0=ct$,
$$\vec{\nabla} \cdot (\vec{\nabla} A^0+\partial_0 \vec{A} )=(\Delta A^0+\partial_0 \partial_i A^i)=-\frac{1}{c} j^0.$$
Now
$$\Delta = \sum_i \partial_i \partial_i=-\partial^i \partial_i,$$
and thus
$$(\partial_i (\partial^i A^0-\partial^0 A^i)=+\frac{1}{c} j^0.$$
This suggests to introduce the antisymmetric Faraday tensor,
$$F^{\mu \nu}=\partial^{\mu} A^{\nu}-\partial^{\nu} A^{\mu} \; \Rightarrow \; \partial_i (\partial^i A^0-\partial^0 A^i) = \partial_{\mu} F^{0 \mu}=\frac{1}{c} j^0. \qquad (*)$$
Now it's clear that we must get also the Maxwell-Ampere law in terms of $F^{\mu \nu}$. Indeed plugging in the potentials gives
$$-\partial_0 (-\partial_0 \vec{A}-\vec{\nabla} A^0)+\vec{\nabla} \times (\vec{\nabla} \times \vec{A})=\frac{1}{c} \vec{j}.$$
Using
$$\vec{\nabla} \times(\vec{\nabla} \times \vec{A})=\vec{\nabla} (\vec{\nabla} \cdot \vec{A})-\Delta \vec{A},$$
written in terms of components we get
$$\partial_0 (\partial^0 A^i - \partial^i A^0) + \partial_j (-\partial^i A^j+\partial^{j}A^i)=\frac{1}{c} j^i$$
or with the Faraday-tensor components
$$\partial_0 F^{0i}+\partial_j F^{ji}=\partial_{\mu} F^{\mu i} =\frac{1}{c} j^i.$$
Together with (*) we thus have also the inhomoegenous Maxwell equations covariant form
$$\partial_{\mu} F^{\mu \nu}=\Box A^{\nu} -\partial^{\nu} \partial_{\mu} A^{\mu}=\frac{1}{c} j^{\nu} \quad \text{with} \quad \Box = \partial_{\mu} \partial^{\mu}.$$
You can use gauge invariance to simplify the equation for the four-vector potential by imposing the Lorenz gauge condition,
$$\partial_{\mu} A^{\mu}=0,$$
leading to
$$\Box A^{\mu}=\frac{1}{c} j^{\mu}.$$
For a free field, $j^{\mu}=0$, the plane-wave solution reads
$$A^{\mu}=a^{\mu} \exp(-\mathrm{i} k \cdot x)$$,
where $a^{\mu}=\text{const}$ and $k=(k^{\mu})=\text{const}$. From $\Box A^{\mu}=0$ one finds
$$k_{\mu} k^{\mu}=0$$
and from the Lorentz-gauge condition
$$k_{\mu} a^{\mu}=k \cdot a=0.$$
The gauge is still not completely fixed, because you can change to another vector potential by
$$A_{\mu}'=A_{\mu} +\partial_{\mu} \chi$$
with an arbitrary scalar field $\chi$ which obeys the wave equation $\Box \chi=0$ without violating the Lorenz-gauge condition. This can be used to arbitrarily set $a^0=0$ ("radiation gauge"), and you are left with two independent components for $a^{\mu}=(0,\vec{a})$ subject to the transversality condition $\vec{k} \cdot \vec{a}=0$.

Now as any other vector field $A^{\mu}$ tansforms under LT's as
$$\bar{A}^{\mu}(\bar{x})={\Lambda^{\mu}}_{\rho} A^{\rho}(x).$$
Thus we have
$$\bar{k}=\hat{\Lambda} k,$$
which includes the Doppler and aberration effect in compact form.

 

[tade]

It is irrelevant because his equations and claims are for plane waves, not spherical waves, and the Wikipedia derivation is also for plane waves. Spherical waves are not considered in either source, so they are not relevant to the comparison of the two sources. It is like reading two travel books on Singapore, getting confused, and then trying to resolve it by asking a question about Hong Kong. Yes, your plane may have flown through Hong Kong to get Singapore, but once there you expect every book to show the same streets.

The four momentum is for a plane wave. Einstein points out that the field far from a source is approximately a plane wave. Einstein uses the plane wave approximation to derive a formula for plane waves which is identical to the plane wave formula used by Wikipedia in another way. Then you are surprised by the fact that the Einstein plane wave equation matches the Wikipedia plane wave equation. This should not be surprising.

I knew that his equation was for plane waves, but spherical waves are relevant to MY question, and that's because it was before I knew that the energy-momentum 4 vectors were just a special case, until PAllen clarified it.

 

[tade]

You can use gauge invariance to simplify the equation for the four-vector potential by imposing the Lorenz gauge condition,
$$\partial_{\mu} A^{\mu}=0,$$
leading to
$$\Box A^{\mu}=\frac{1}{c} j^{\mu}.$$
For a free field, $j^{\mu}=0$, the plane-wave solution reads
$$A^{\mu}=a^{\mu} \exp(-\mathrm{i} k \cdot x)$$,

Am I right to say that at this step the EM field reduces to a four-vector approximation?

...for one particular purpose, calculating the Doppler shift of the radiation, using a 4-vector is a good enough approximation far away from the source...

 

[vanhees71]

It's not an approximation, it's a special solution of the free Maxwell equations. Of course, plane waves are never realized in nature, but you can use them to build any em. field by "superposition" (or, more precisely, as a Fourier integral).

 

[tade]

place set

 

[Dale]

that's because it was before I knew that the energy-momentum 4 vectors were just a special case, until PAllen clarified it.

Ok, that makes sense.

 

[PeterDonis]

so that's what PAllen meant by classical massless particle.

Not quite.

A plane wave solution of the source-free Maxwell's Equations is a pair of 3-vectors $\vec{E}$, $\vec{B}$ such that $\vec{E} \cdot \vec{B} = 0$ and both vectors can be written as linear combinations of $e^{i \left( \vec{k} \cdot \vec{x} - \omega t \right)}$ and $e^{- i \left( \vec{k} \cdot \vec{x} - \omega t \right)}$, where $\vec{E} \cdot \vec{k} = \vec{B} \cdot \vec{k} = 0$ and $\omega^2 = k^2$.

A classical massless particle is a point particle described by a 4-vector $P^{\mu} = (E, \vec{p})$ such that $P^{\mu} P_{\mu} = E^2 - p^2 = 0$; or, equivalently, a 3-vector $\vec{p}$ and an energy $E$ that satisfies $E^2 = p^2$.

The plane wave solution contains more information than the classical massless particle. We can form the vector $\vec{E} \times \vec{B}$ and show that it is a 3-vector $\vec{p}$ with an associated energy $E$ that satisfies the classical massless particle relation above. But there is additional information not captured by doing this: the polarization of the wave, i.e., the phase relationship between $\vec{E}$ and $\vec{B}$.

 

[vanhees71]

I see, so that's what PAllen meant by classical massless particle.

No, please forget classical massless particles in the context of electromagnetic waves. It's much simpler to talk about well-defined things. Classical massless particles are not a good model of electromagnetic waves at all.

 

[tade]

The plane wave solution contains more information than the classical massless particle. We can form the vector $\vec{E} \times \vec{B}$ and show that it is a 3-vector $\vec{p}$ with an associated energy $E$ that satisfies the classical massless particle relation above. But there is additional information not captured by doing this: the polarization of the wave, i.e., the phase relationship between $\vec{E}$ and $\vec{B}$.

'
yep understood

 

[tade]

No, please forget classical massless particles in the context of electromagnetic waves. It's much simpler to talk about well-defined things. Classical massless particles are not a good model of electromagnetic waves at all.

Yeah, but they are good for highlighting the wave-particle nature of photons though.

 

[vanhees71]

Argh! The point is that you never ever should highlighting something that doesn't exist anymore in physics for about 90 years. There is no wave-particle nature of photons nor other field quanta. The socalled "wave-particle dualism" was an important heuristic before modern quantum theory has been discovered. Planck who discovered "photons" in a sense in 1900 was right in fighting against the "light-particle point of view" promoted by Einstein, and also Einstein himself was very aware of his idea being "heuristic". That's, by the way the title of the paper, where he introduces his light-particle idea when "explaning" the photoelectric effect. The title of the paper is "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" (About a heuristic aspect concerning the production and change of light; translation mine). He was well aware that this idea was not a fully satisfactory theory of light in terms of "particles". Nowadays we know that the photoelectric effect is not primarily due to the quantum aspects of the electromagnetic field but can be understood from the quantization of the electrons in the metal interacting with a classical electromagnetic wave. Despite the ingenious development of early quantum theory by Planck, Einstein, and Bohr the much more satisfying solution of the puzzling behavior of things at the atomic and subatomic scale is modern quantum theory, developed independently (with an important contribution from de Broglie in form of his doctoral thesis, where "particles" like electrons were described as waves, i.e., the wave-particle-duality idea ("heuristic"!) applied to "particles" in analogy to Einsteins light quanta where "particle" aspects were attributed to the wave phenomenon light) by Heisenberg+Born+Jordan, Dirac, and Schrödinger.

 

[tade]

...We can form the vector $\vec{E} \times \vec{B}$ and show that it is a 3-vector $\vec{p}$ with an associated energy $E$ that satisfies the classical massless particle relation above.

In that same paper, Einstein derived an expression for relativistic KE, which has been applied to classical massless particles.

We will now determine the kinetic energy of the electron. If an electron moves from rest at the origin of co-ordinates of the system K along the axis of X under the action of an electrostatic force X, it is clear that the energy withdrawn from the electrostatic field has the value

. As the electron is to be slowly accelerated, and consequently may not give off any energy in the form of radiation, the energy withdrawn from the electrostatic field must be put down as equal to the energy of motion W of the electron. Bearing in mind that during the whole process of motion which we are considering, the first of the equations (A) applies, we therefore obtain

Einstein did this by using the E and B field transformations:

He plugged these transformations into the Lorentz force law in order to determine how a force transforms between frames.

From that he was able to derive an expression for KE.How might this derivation be modified in order to accurately account for the Doppler shifts of spherical wavefronts instead of just plane waves?

 

[Dale]

Einstein did this by using the E and B field transformations:
...
How might this derivation be modified in order to accurately account for the Doppler shifts of spherical wavefronts instead of just plane waves?

Probably start with the E and B field for your spherical wavefront and transform those instead. Maybe the standard dipole field wold be best. The math would get annoying pretty fast.

 

[tade]

Probably start with the E and B field for your spherical wavefront and transform those instead. Maybe the standard dipole field wold be best.

Do these apply to spherical wavefronts?

 

[Dale]

Do these apply to spherical wavefronts?

Not as written since the fields are written only as functions of x. I would construct the EM tensor and use that instead.

 

[tade]

Not as written since the fields are written only as functions of x. I would construct the EM tensor and use that instead.

oh f***, I'm so dumb.

https://en.wikipedia.org/wiki/Class...rmation_of_the_fields_between_inertial_frames

I thought that the transformations applied to all points in space, and the Wikipedia article didn't make it clear that it was only for x.