Static Equilibrium: Proving Forces are Equal

[astr0]

Three forces act on an object in static equilibrium.

(a) If F1 and F2 represent the magnitudes of the forces acting on the object, show that

.

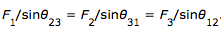(b) Show that

I know that the sum of all forces needs to be zero if the system is in equilibrium, but I don't know how to prove that each force divided by the sine of theta is equal to each other.

 

[ashishsinghal]

when you add three forces (in representation ) which are in equilibrium, you get a triangle
this is because the net magnitude is zero. Draw such a diagram and then solve the question