Camailee
- 2
- 0
- Homework Statement
- The ramp ABCD is supported by cables at corners C and D. The tensile force in both cables is 420N. Determine the moment about point A produced by the force exerted at point C.
- Relevant Equations
- Moment at A (MA) = rGA x TCG.
Where rGA = GA/|GA|
TCG = 420N
Problem illustration:
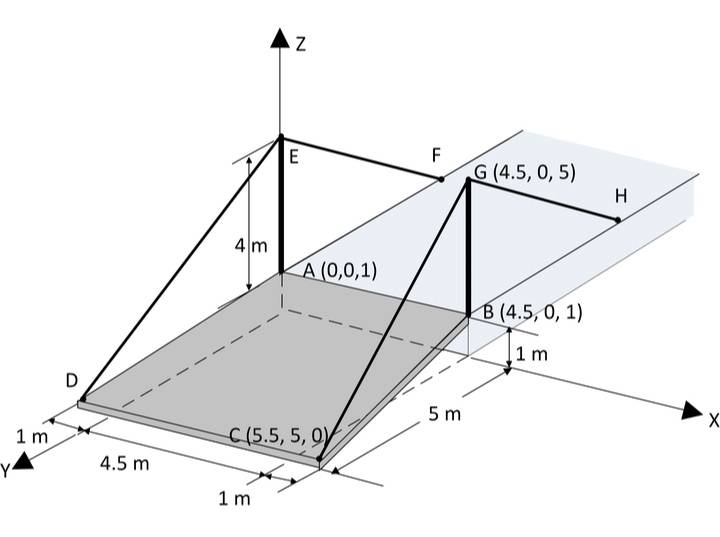
The possible answers are:

I don't understand why it says Mc if it is asking for the moment at A, not C. But maybe I am getting something wrong.
So with the formulas I posted above, I have this:
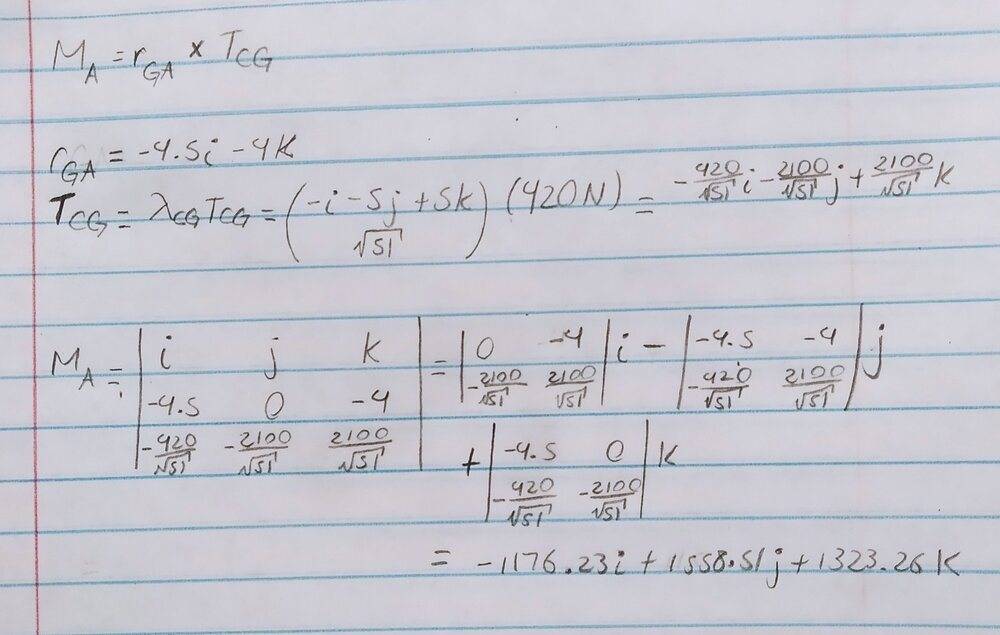
The possible answers are:
I don't understand why it says Mc if it is asking for the moment at A, not C. But maybe I am getting something wrong.
So with the formulas I posted above, I have this:
Last edited by a moderator: