Help needed with a Statics Question: Load is supported by a Pulley and Cables

[MecEngPterois]

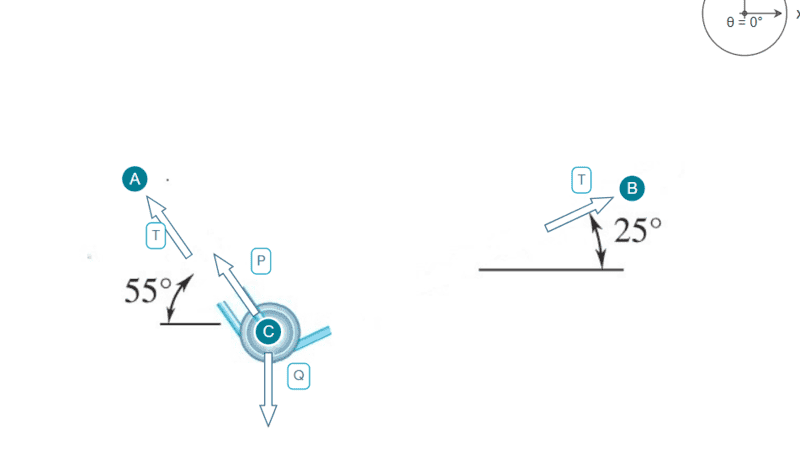
What I did was split the problem into two seperate summations based on x & y coordinates:

Tcos(25) - Tcos(55) - Px = 0
Tsin(25+Tsin(55) +Py - Q = 0,

Where Q = 1860

I initially got an answer of 2391N, but it keeps marking me wrong for said answer.

This is the free body diagram, (the previous question asked me to construct) that I am basing my work off of:

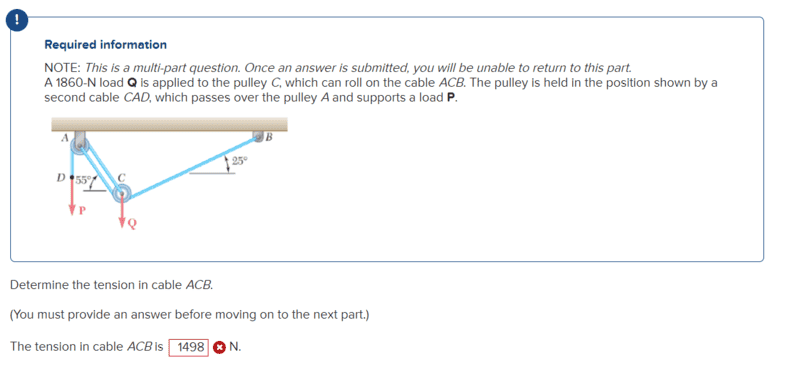
Here is the question.

 

[Lnewqban]

Welcome, @MecEngPterois !

Could you show us your work in detail?

Think of the principle behind a bow and an arrow.
Is it easier for the hand to initiate the pulling of the cord than directly bending the bow?

 

[Chestermiller]

The horizontal and vertical force balances on the pulley F should read:
$$T\cos{25}-(T+P)\cos{55}=0$$. $$T\sin{25}+(T+P)\sin{55}-Q=0$$

 

[Lnewqban]

@MecEngPterois
Could you find the correct solution?