- #1
starryeyed
- 3
- 0
Homework Statement
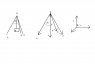
A weight of 10 N is hanging from the top of a three-legged support. The legs are attached to the horizontal floor and form equal angles with each other. Find the forces in the legs, if they form an angle of 30 degrees with the rope.
Homework Equations
[tex]\sum[/tex]Fx=0
[tex]\sum[/tex]Fy=0
[tex]\sum[/tex]Fz=0
The Attempt at a Solution
I'm lost. Maybe I should just give up on the whole topic of statics, I've never had this much difficulty with any other subject in physics. I understand the examples and the stuff in the book but I can't seem to solve any problems on my own. I'm not sure if these are even correct. Sum of the projections of the vectors-
BAsin30+BCsin30+BDsin30=0 The projections of P and BE are zero, since they are at a 90 degree angle with x.
BAcos30+BCcos30+BDcos30+BE+10=0
BAcos15+BCcos15+BDcos15+BEcos45+10cos45=0
The 15 is there, because I figured they were at a 15 degree angle with z.
I don't know if BA, BC and BD are all supposed to be equal:S
Anyways, help would be very much appreciated:)
 )
)