Steady State Error of a PI Controlled System (parabolic input)

[Saam]

Hey guys/gals,

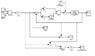
The block diagram attached is a PI controlled robotic joint system where:

G(s)=Kp+(Ki/s)
P(s)=48500/(s^2+2.89s)

R(s)= joint’s desired angular position
C(s)= joint’s angular position
D(s)= external disturbance
G(s)= PI controller
ess= Steady State Error

My problem:
A) Find the value Ki that will result in ess=5% for a parabolic input.
B) Using this value of Ki find the range of Kp for closed-loop stability.

My solution:

ess=1/Ka=0.05

Ka=lim(s>0) s^2G(s)P(s)=20

G(s)P(s)=((sKp+Ki)/s)(48500/(s^2+2.89s))
=(48500sKp+48500Ki)/(s^3+2.89s^2)
=(48500sKp+48500Ki)/(s^2(s+2.89))

Ka=48500Ki/2.89=20
Ki=20*2.89/48500
Ki=0.0011917

I tried using this Ki value in my Simulink model (other attachment) but the system didn’t have any steady state error, and I could only manage to get steady state error by making Ki = 0.
Also, I didn’t know how to insert a parabolic input into Simulink so I used this instead:
Ramp x Ramp x 0.5 to represent (½)t^2

My questions:
1) Is my parabolic input correct?
2) Is my PI controller set out correctly in my Simulink model? (I wasn’t sure how to model the I component)
3) For this part of the question I’ve been ignoring the disturbance (D(s)), it’s not mentioned in this part, is it ok to ignore?
4) Am I going about finding Ki the right way?
5) What path should I take to get Kp after I have Ki? I’m thinking I need to do a Routh array.

Looking for a little nudge toward the right path.

Thanks for the help,
Sam

 

[viscousflow]

1) try two transfer function blocks [1/s] in series. (Although I suspect what you're doing is equivalent)

2) It is correct, although there is PID controller block.

3) There is no model of D(s) given so you can assume nothing helpful.

4) Looks like you're on the right track but its too late to check numbers right now.

5)You can do that.

Hint: You can check your answer (or solve the problem) using sisotool.