- #1
annas425
- 17
- 0
Matlab Simulink--Using PID controls?
I need to use Simulink to determine an approximate numerical solution to the equation of motion for a robotic arm (image below). The equation of motion for the system is J (\theta)'' = \tau - mgl cos (\theta). (An ordinary, 2nd order nonlinear differential equation.)
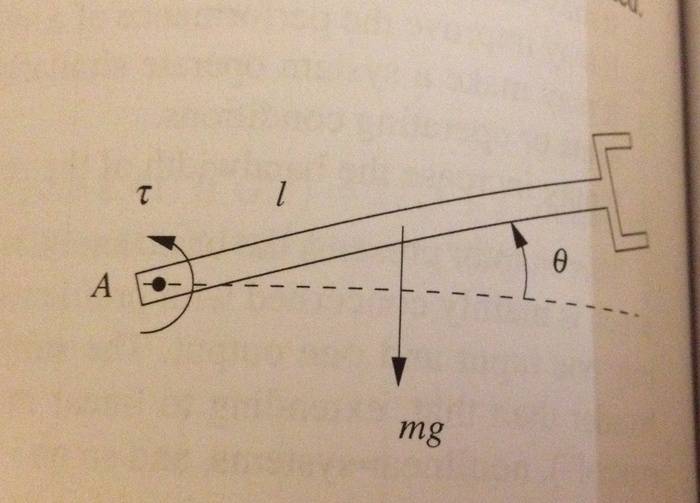
Assuming zero initial conditions and a small desired angle of the robot arm, I need to verify the following rules of thumb for PID control for a step input.
- for proportional control (Kp > 0, Kd = 0, Ki = 0), the solutions are oscillatory, and Kp increases the frequency of oscillation (which decrease the rise time and peak time), but decreases the mean steady state error. The settling time is finite (Hint: pick a starting value of Kp = 5)
- Add derivative control to the proportional controller (i.e., Kp > 0, Kd > 0, Ki = 0) and verify the following:
a) for small Kd, solutions are decaying oscillations
b) increasing Kd deceases settling time
c) increasing Kd to sufficiently large value eliminates oscillatory behavior; solution
experimentally decays to final steady state value.
d) increasing Kp decreases the final steady state error
e) increasing Kp decreases rise time
(Hint: pick a starting value of Kd = 0.5)
I am really struggling with how to use Simulink, and especially how to do this in Simulink. Any tips/advice for a starting place to solve this problem would be GREATLY appreciated! I would really, sincerely appreciate any and all help with this! Thank you!
It's hard for me to give an "attempt at a solution" when I am completely lost :( I am not asking for the answer, I just want to know where to begin. Please please, understand. I understand the relationships between items (a) through (d), but I do not know how to even begin to use Simulink, or model this equation in Simulink. Thank you again in advance.
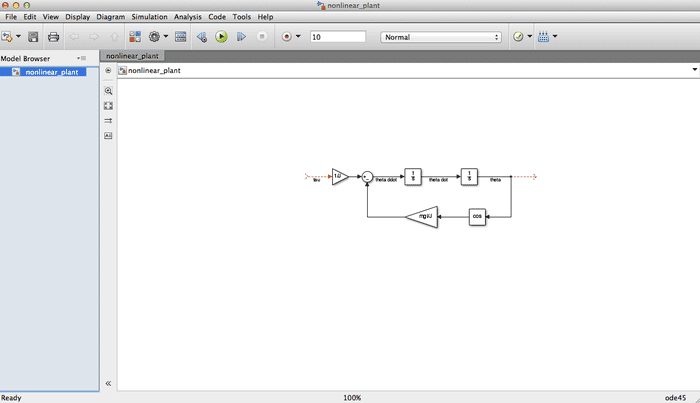
Here is a screenshot of a .slx Simulink file that my professor sent out in order to help us with the nonlinear model…I'm not sure what to do with it (when I run it, it says that "J is an undefined variable"):
I need to use Simulink to determine an approximate numerical solution to the equation of motion for a robotic arm (image below). The equation of motion for the system is J (\theta)'' = \tau - mgl cos (\theta). (An ordinary, 2nd order nonlinear differential equation.)
Assuming zero initial conditions and a small desired angle of the robot arm, I need to verify the following rules of thumb for PID control for a step input.
- for proportional control (Kp > 0, Kd = 0, Ki = 0), the solutions are oscillatory, and Kp increases the frequency of oscillation (which decrease the rise time and peak time), but decreases the mean steady state error. The settling time is finite (Hint: pick a starting value of Kp = 5)
- Add derivative control to the proportional controller (i.e., Kp > 0, Kd > 0, Ki = 0) and verify the following:
a) for small Kd, solutions are decaying oscillations
b) increasing Kd deceases settling time
c) increasing Kd to sufficiently large value eliminates oscillatory behavior; solution
experimentally decays to final steady state value.
d) increasing Kp decreases the final steady state error
e) increasing Kp decreases rise time
(Hint: pick a starting value of Kd = 0.5)
I am really struggling with how to use Simulink, and especially how to do this in Simulink. Any tips/advice for a starting place to solve this problem would be GREATLY appreciated! I would really, sincerely appreciate any and all help with this! Thank you!
It's hard for me to give an "attempt at a solution" when I am completely lost :( I am not asking for the answer, I just want to know where to begin. Please please, understand. I understand the relationships between items (a) through (d), but I do not know how to even begin to use Simulink, or model this equation in Simulink. Thank you again in advance.
Here is a screenshot of a .slx Simulink file that my professor sent out in order to help us with the nonlinear model…I'm not sure what to do with it (when I run it, it says that "J is an undefined variable"):
Last edited: