Steam flow rate in 2-chamber steam engine system

[Denniskwantas]

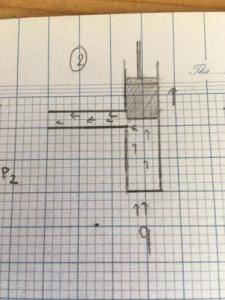
Our system of interest has a duct on the left and a piston chamber on the right that make the shape of the letter T rotated 90º clockwise. The smaller tube on the left is abbreviated as P1 has an unspecified length while the piston chamber is P2. The air in P2 heats up and expands while the pressure remains constant (isobaric process). That said, heat energy (q) is supplied to the piston chamber to heat up the air and lift the piston up simultaneously.

In phase 2, the heated air escapes to P1 via the opening and heat energy is still supplied to the chamber to continue lifting the piston up. Caveat: The volumetric flow rate between P1 and P2 is not conserved because part of it goes to lifting the piston.

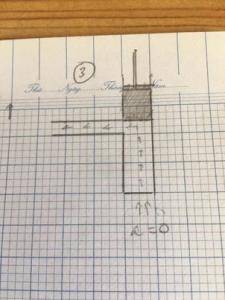
In phase 3, the heat supply is cut off and the position of the piston is locked in by some mechanism. The heat and vapor accrued in the isobaric expansion process in P1 will flow to P2.

The question is conceptual rather than finding the exact number. How can I find the flow rate of the steam as it enters P2 in phase 2 and when the piston's position is locked in phase 3 ?

Here are all the relevant equations, rewritten in LaTex.

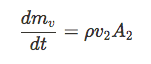
This is the general equation for mass flow rate which equals to the product of steam density, steam velocity and the area of the opening between P1 and P2 .

Recently I've found another equation for steam flow rate in a pipe.
https://www.physicsforums.com/attachments/291039

d : Pipe Inner Diameter (m)
v : Steam Velocity (m/s)
V : Specific volume (m³/kg)
m_s : Steam Flow Rate (kg/h)

Source: TLV

 

[Chestermiller]

You refer to air. Did you mean steam?

 

[Denniskwantas]

Yep. Steam it is. But it's not boiling steam though.

 

[Chestermiller]

And what is the boundary condition at the far end of P1? Is it dead ended, or is it at constant pressure? Or something else?

 

[Denniskwantas]

As for the boundary conditions though, the P1 tube would be twice as long as P2 and yes, the P1 is at constant pressure with P2 as well.

I'm really interested in knowing whether the expansion of the heated moist air could lift the piston in P2 in any capacity.