Discussion Overview
The discussion revolves around the forces involved in steering a car, particularly focusing on the gyroscopic effects of spinning wheels and how they influence the ability to rotate the wheels for steering. Participants explore the relationship between applied torque and resultant rotation while considering constraints on movement.
Discussion Character
- Exploratory
- Technical explanation
- Conceptual clarification
- Debate/contested
Main Points Raised
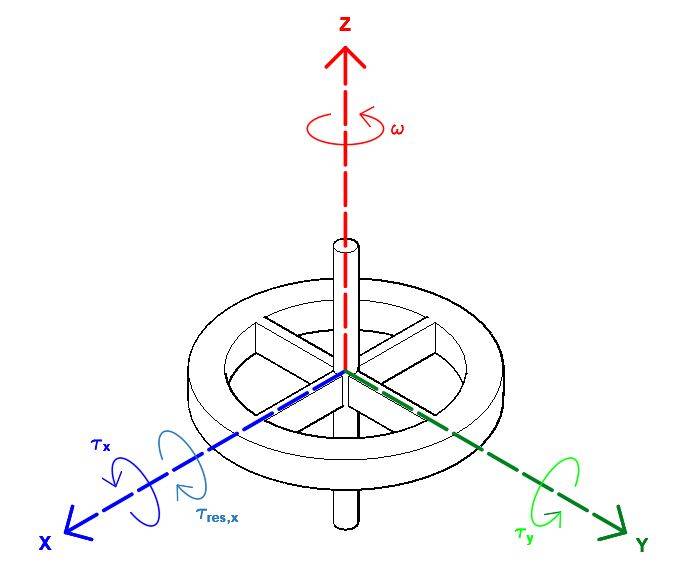
- One participant questions whether the gyroscopic effect of spinning wheels creates a force that opposes the rotation needed for steering, seeking to quantify this opposition.
- Another participant suggests that the resistance to turning the wheels includes both the gyroscopic effect and additional resistance from the steering system's geometry, which tends to return the wheels to a straight direction.
- A participant expresses concern about understanding the relationship between the torque applied on the X axis and the resulting rotation about X, while keeping Y constrained, noting their background in electrical engineering rather than physics.
- A later reply references historical aircraft design to draw parallels with automobile steering dynamics, suggesting that similar gyroscopic effects may influence vehicle behavior, particularly in terms of directional bias.
Areas of Agreement / Disagreement
Participants do not reach a consensus on the specifics of the gyroscopic effect's influence on steering, and multiple competing views regarding the nature of resistance and its implications remain present.
Contextual Notes
Participants acknowledge limitations in their understanding of the gyroscopic effects and the complexities involved in quantifying the relationship between torque and rotation, particularly under constrained conditions.
Who May Find This Useful
This discussion may be of interest to individuals studying vehicle dynamics, physics students exploring rotational motion, and engineers considering the implications of gyroscopic effects in mechanical systems.