Rectifier
Gold Member
- 313
- 4
The problem
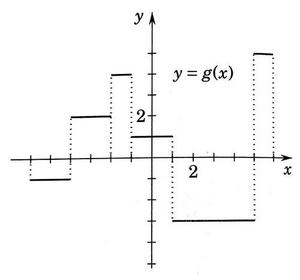
I want to calculate ## \int^6_{-6} \frac{g(x)}{2+g(x)} \ dx ## for the step function below.
 The attempt
The attempt
I started with rewriting the function as with the help of long-division
## \int^6_{-6} \frac{g(x)}{2+g(x)} \ dx = \int^6_{-6} 1 \ dx - 2\int^6_{-6} \frac{1}{g(x)+2} \ dx##
I know that ##\int^6_{-6} 1 \ dx = 12## but that's about it. I am not sure how I should continue.
And here is where I get stuck.
I want to calculate ## \int^6_{-6} \frac{g(x)}{2+g(x)} \ dx ## for the step function below.
I started with rewriting the function as with the help of long-division
## \int^6_{-6} \frac{g(x)}{2+g(x)} \ dx = \int^6_{-6} 1 \ dx - 2\int^6_{-6} \frac{1}{g(x)+2} \ dx##
I know that ##\int^6_{-6} 1 \ dx = 12## but that's about it. I am not sure how I should continue.
And here is where I get stuck.
Last edited: