BareFootKing
- 30
- 0
I am having trouble understand why
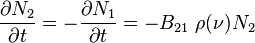 is true I would think that the rate in which N2 is changing is the rate of stimulated emission and spontanous emission together. Why is it just the rate of stimulated emission
is true I would think that the rate in which N2 is changing is the rate of stimulated emission and spontanous emission together. Why is it just the rate of stimulated emission
It is in the mathematical model section
http://en.wikipedia.org/wiki/Stimulated_emission
It is in the mathematical model section
http://en.wikipedia.org/wiki/Stimulated_emission