JBD
- 15
- 1
As shown in the image below, I tried to integrate a large integral. However, the result is strange. According to the result, the integral is always zero whatever the values of w, h, L, P, S and k. However, when I try to put some "test values", the result is not zero.
test values: P=1,w=1,h=0.1,L=1,S=0,k=0.2
This is not consistent with ouput 1. So what's wrong with my first input?
Codes:
Integrate[P/((Sqrt[y^2 + L^2 + z^2]) ((S - y)^2 + P^2 + z^2))Cos[k (Sqrt[y^2 + L^2 + z^2] +
Sqrt[(S - y)^2 + P^2 + z^2])], {y, -w/2, w/2}, {z, -h, h}]
NIntegrate[1/((Sqrt[y^2 + 1^2 + z^2]) ((0 - y)^2 + 1^2 + z^2))Cos[0.2 (Sqrt[y^2 + 1^2 + z^2] +
Sqrt[(0 - y)^2 + 1^2 + z^2])], {y, -0.5, 0.5}, {z, -0.1, 0.1}]
NIntegrate[Cos[0.4 Sqrt[1 + y^2 + z^2]]/(1 + y^2 + z^2)^(3/2), {y, -0.5, 0.5}, {z, -0.1, 0.1}]
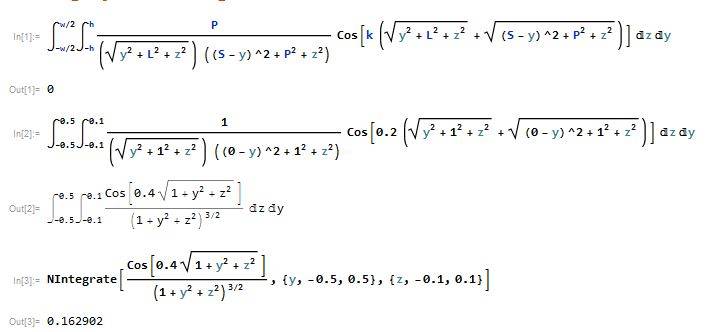
test values: P=1,w=1,h=0.1,L=1,S=0,k=0.2
This is not consistent with ouput 1. So what's wrong with my first input?
Codes:
Integrate[P/((Sqrt[y^2 + L^2 + z^2]) ((S - y)^2 + P^2 + z^2))Cos[k (Sqrt[y^2 + L^2 + z^2] +
Sqrt[(S - y)^2 + P^2 + z^2])], {y, -w/2, w/2}, {z, -h, h}]
NIntegrate[1/((Sqrt[y^2 + 1^2 + z^2]) ((0 - y)^2 + 1^2 + z^2))Cos[0.2 (Sqrt[y^2 + 1^2 + z^2] +
Sqrt[(0 - y)^2 + 1^2 + z^2])], {y, -0.5, 0.5}, {z, -0.1, 0.1}]
NIntegrate[Cos[0.4 Sqrt[1 + y^2 + z^2]]/(1 + y^2 + z^2)^(3/2), {y, -0.5, 0.5}, {z, -0.1, 0.1}]