- #1
etotheipi
For instance, consider two sources of light ##S_{1}## and ##S_{2}## where ##S_{1}## is emitting with a phase angle ##\frac{\pi}{4}## greater than ##S_{2}##. The light from ##S_{1}## travels a straight distance ##d_{1}## through a medium of refractive index ##n_{1}##. The light from ##S_{2}## travels a total distance ##d_{2}## through a medium of refractive index ##n_{2}##, reflecting off of a plane mirror as well. Please see the below diagram:
(N.B. I forgot to draw in a barrier, but assume light cannot travel directly from ##S_{2}## to X!)
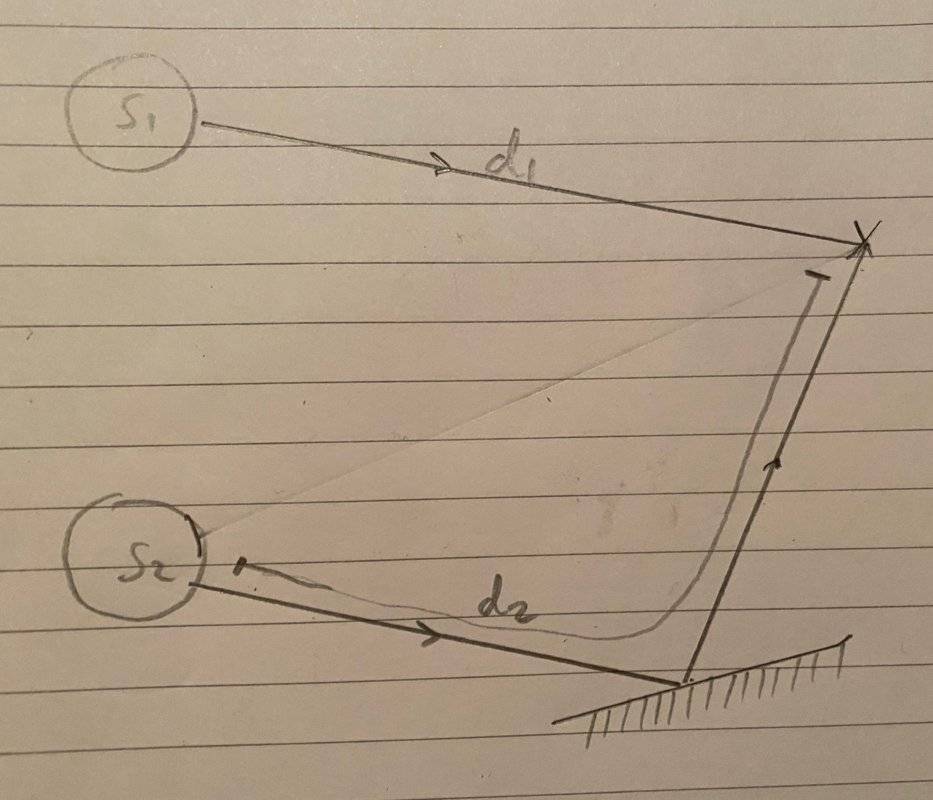
Let's say we want constructive interference at X where the rays meet. The strategy I came up with is keeping track of the phase angle (modulo an uninteresting ##2\pi##) of each light ray at points along the path of each. So I would say that if we set the phase of ##S_{1}## to ##\frac{\pi}{4}## at some constant time, the phase angle at X on the first light ray would be
##\phi_{1} = \frac{\pi}{4} + 2\pi\frac{OPL_{1}}{\lambda}## (where ##\frac{OPL}{\lambda} = \frac{n_{1}d_{1}}{\lambda}## is the number of wavelengths along the path).
whilst the phase at X on the second wave would be
##\phi_{2} = 0 + 2\pi\frac{OPL_{2}}{\lambda} + \frac{\pi}{2}## (with the final term due to the reflection).
Finally, I'd set the difference to be a multiple of ##2\pi## and would go from there to solve the system. I can't help but think this is a really convoluted way of going about the question, and I was wondering if anyone had a better method? Thank you in advance!
(N.B. I forgot to draw in a barrier, but assume light cannot travel directly from ##S_{2}## to X!)
Let's say we want constructive interference at X where the rays meet. The strategy I came up with is keeping track of the phase angle (modulo an uninteresting ##2\pi##) of each light ray at points along the path of each. So I would say that if we set the phase of ##S_{1}## to ##\frac{\pi}{4}## at some constant time, the phase angle at X on the first light ray would be
##\phi_{1} = \frac{\pi}{4} + 2\pi\frac{OPL_{1}}{\lambda}## (where ##\frac{OPL}{\lambda} = \frac{n_{1}d_{1}}{\lambda}## is the number of wavelengths along the path).
whilst the phase at X on the second wave would be
##\phi_{2} = 0 + 2\pi\frac{OPL_{2}}{\lambda} + \frac{\pi}{2}## (with the final term due to the reflection).
Finally, I'd set the difference to be a multiple of ##2\pi## and would go from there to solve the system. I can't help but think this is a really convoluted way of going about the question, and I was wondering if anyone had a better method? Thank you in advance!
Attachments
Last edited by a moderator:
