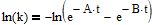Stuck Trying to Re-arrange Variables

[cgw_niu]

Homework Statement

I need to re-arrange the below statement in terms of "t"

Relevant Equations

Original Equation:

k = 1/[e^(-A*t) - e^(-B*t)]

Where k is a real number and A and B are real numbers > 1

this is as far as I get:

 

[cgw_niu]

Here is the original form of the equation

 

[HallsofIvy]

I doubt you will find any algebraic solution to that equation.

 

[cgw_niu]

I doubt you will find any algebraic solution to that equation.

bummer, I am often given the value of "k" but do not know at what time it happens. The only was so far is to plug and play or plot it and get a close estimate for "t". I am by far means no mathematician, but I would think there has to be a way to solve for "t" for a known value of "k". Maybe not though.

 

[phyzguy]

It's easy to solve for t numerically given the other values. A method like Newton's method should converge to a solution rapidly. That's probably what you really want.