Switching between distance variables in a simple seismograph

  • Context: Undergrad 
  • Thread starter Thread starter shanepitts
  • Start date Start date
  • Tags Tags
    Variables
Click For Summary

Discussion Overview

The discussion revolves around the substitution of distance variables in the context of a seismograph problem presented in a textbook. Participants are exploring the reasoning behind replacing the y variable with x, as illustrated in specific figures from the textbook, and the implications of these substitutions on the equations governing motion.

Discussion Character

  • Technical explanation
  • Mathematical reasoning
  • Homework-related

Main Points Raised

  • One participant expresses confusion regarding the substitution of the y variable with x as per figure 3.6.3.
  • Another participant suggests that figure 3.2.5 may clarify the substitution process.
  • A third participant reiterates the suggestion about figure 3.2.5, indicating ongoing confusion.
  • A later reply explains the substitution of variables in detail, referencing Newton's 2nd law and providing equations to illustrate the simplification process.
  • The explanation includes a step-by-step derivation of the equations, concluding that the resulting equation (Eq. 3) is simpler than the original (Eq. 1).
  • The participant assumes that the textbook contains all necessary information to understand these substitutions.

Areas of Agreement / Disagreement

Participants do not appear to reach a consensus on the clarity of the figures or the substitutions, as confusion persists despite attempts to explain the process. Multiple viewpoints regarding the effectiveness of the figures in clarifying the problem remain evident.

Contextual Notes

Some participants may be missing assumptions or context provided in the textbook, which could affect their understanding of the substitutions and the equations involved. The discussion does not resolve the confusion expressed by the initial poster.

shanepitts
Messages
84
Reaction score
1
Below is an example problem from my textbook. I don't fathom the highlighted portion where they replace the y variable with x in accordance with fig. 3.6.3?

Please help

Thanks

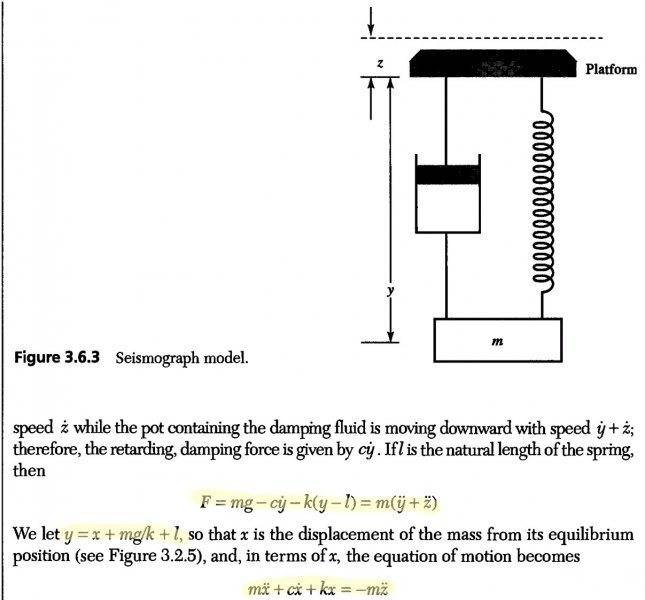
image.jpg
image.jpg
 
Physics news on Phys.org
Doesn't figure 3.2.5 explain it?
 
  • Like
Likes   Reactions: shanepitts
paisiello2 said:
Doesn't figure 3.2.5 explain it?

Here is the other Figure. Unfortunately, I still don't fathom??
image.jpg
 
In figure 3.2.5 they are simply substituting in X'e to simplify the equation. From Newton's 2nd law of motion:
∑F = m⋅d2X/dt2
m⋅d2X/dt2 = mg - k(X - Xe) ...(Eq. 1)

At equilibrium we know that ∑F = 0, therefore:
mg - k(X - Xe) = 0
→ X - Xe = mg / k ...(Eq. 2)

Making the following two substitutions into (Eq. 1):
Xe = X'e - mg/k
X = X'e + x
→ m⋅d2(X'e + x)/dt2 = mg - k((X'e + x) - (X'e - mg/k))
→ m⋅d2(x)/dt2 = mg - kx + mg
→ m⋅d2x/dt2 = kx ...(Eq. 3)

Now Eq.3 is simpler than Eq. 1, agreed?

I assume your textbook already has all this.
 
  • Like
Likes   Reactions: shanepitts

Similar threads

Undergrad Statistical modeling and relationship between random variables
  • · Replies 7 ·
Replies
7
Views
2K
Undergrad Variable Normalization for different variable ranges....
  • · Replies 3 ·
Replies
3
Views
2K
Undergrad Count and Categorical Variables...
  • · Replies 3 ·
Replies
3
Views
2K
Change of variable for Jacobian: is there a method?
  • · Replies 5 ·
Replies
5
Views
2K
Undergrad Quick Change of Variables Question
  • · Replies 15 ·
Replies
15
Views
2K
Undergrad Sample space, outcome, event, random variable, probability...
  • · Replies 6 ·
Replies
6
Views
3K
Undergrad Is the fork in the Einstein Podolsky Rosen argument correct?
  • · Replies 45 ·
2
Replies
45
Views
3K
Undergrad EM equations - am I missing something?
  • · Replies 4 ·
Replies
4
Views
1K
Graduate Resonant frequencies of liquid in a cylinder
  • · Replies 14 ·
Replies
14
Views
3K
Undergrad Ads/CFT and Ashtekar variables or spinfoam
  • · Replies 7 ·
Replies
7
Views
3K