LagCompensator
- 24
- 1
1. Problem Statement:
A 4-pole, star-connected, 50 Hz, 11kV, 40 MVA turbogenerator, with a synchronous reactance of 0.8 p.i., is connected to a power network. This power network can be represented by 11-kV infinite bus with a series reactance of j 0.5 Ω. A voltage regulator adjusts the field current such that alternator terminal voltage remains constant at 11 kV.
2. Relevant equation:
Based on the information above I can write the following equation:
\overline{E}_ f= \underbrace{\overline{V}_{bus} + jX_{line}\overline{I}_a}_{V_t} + jX_{s}\overline{I}_a
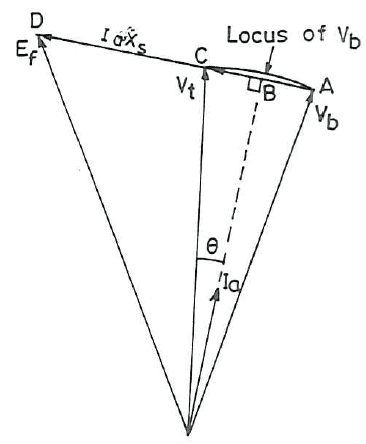
Based on the equation above I can draw the following phasor diagram. I just copied the one drawn in the book, due to my paint skills did not yield a pretty result.
The phasor diagrams draws I_a lagging with respect to V_t, and therefore \theta is the angle between them.
My question is: How do I know how to draw I_a? I know that I_a should atleast be lagging V_t at lagging power factor, but could it not also be drawn lagging with respect to V_b and then \theta is the angle between V_b and \theta?
I guess \theta is defined from V_t is because V_t is chosen as reference phasor. But I am still confused by how I_a is placed.
Hope I made myself clear, and appreciate any help, best regards.
A 4-pole, star-connected, 50 Hz, 11kV, 40 MVA turbogenerator, with a synchronous reactance of 0.8 p.i., is connected to a power network. This power network can be represented by 11-kV infinite bus with a series reactance of j 0.5 Ω. A voltage regulator adjusts the field current such that alternator terminal voltage remains constant at 11 kV.
2. Relevant equation:
Based on the information above I can write the following equation:
\overline{E}_ f= \underbrace{\overline{V}_{bus} + jX_{line}\overline{I}_a}_{V_t} + jX_{s}\overline{I}_a
The Attempt at a Solution
:[/B]Based on the equation above I can draw the following phasor diagram. I just copied the one drawn in the book, due to my paint skills did not yield a pretty result.
The phasor diagrams draws I_a lagging with respect to V_t, and therefore \theta is the angle between them.
My question is: How do I know how to draw I_a? I know that I_a should atleast be lagging V_t at lagging power factor, but could it not also be drawn lagging with respect to V_b and then \theta is the angle between V_b and \theta?
I guess \theta is defined from V_t is because V_t is chosen as reference phasor. But I am still confused by how I_a is placed.
Hope I made myself clear, and appreciate any help, best regards.