System Identification: Finding Transfer Function w/ Graphical Methods

[HWGXX7]

Hello,

I have to find the transfer function of a given model (matlab). My task is to determine this function, by means of a step response of the system. I have to use graphical methods tot get the parameters, the proces itself is a high order proces with non minimum phase.

G(s)=K.\frac{(1-Ts)}{(1-\tau s)^{n}}
My first attempt (the blue curve isn't very accurate. Someone whith experience who can help me out?

To situate my problem: I have have to find the proces-parameters witch graphical data. Problem is, this isn't very accurate at all..So I'm kinda gambling...But is what I wrote down correct for this process?

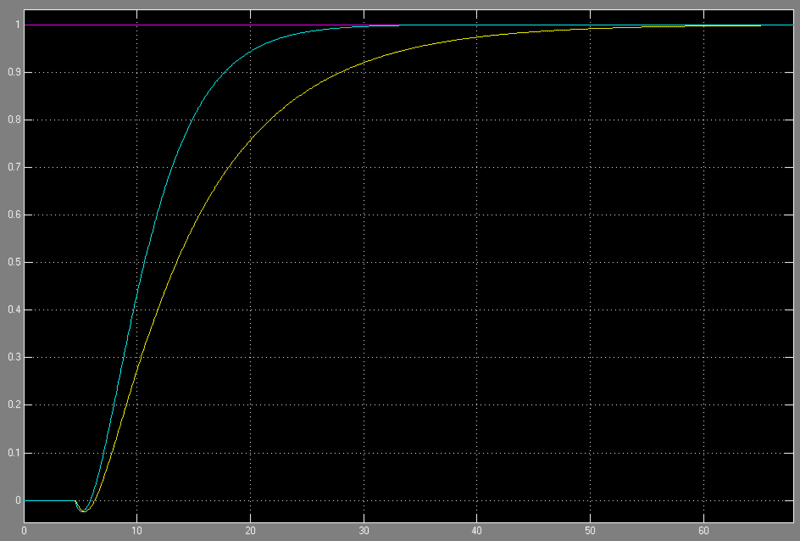
Aprreciate help!

grtz

 

[Floid]

Probably not much help here but since no one else has thrown anything out there:

The only time I have tried something like that I did a bit of trial and error coupled with knowledge of what changing a transfer functions parameters can cause.

So for example if you want to move the blue line closer to the yellow line and you are using a second order denominator like

10
--------------
s^2 + 5s + 10

then increasing the first order term (5s) would stretch out the slope of the curve. So for example 7s as the first order term in the above equation would stretch it out.

You may try playing with the transfer function by hand like that to get the desired result. Sorry if this isn't really what you were asking.

 

[HWGXX7]

I'm following a electromechanical course with some advanced courses of feedback systems. This is a exam for which I have to set up a good PID control system. Problem is I can't find the 'exact' transferfunction, which kill al the other question of course..

What you wrote down (second order denominator) is indeed a way to find the proces function and the proces parameters. trial and error works grate with experience and some knowledge of basis function.

Problem is that this system is little more advanced and just by t&e I won't find the correct proces..
But thank anyway for your reply.