System of hollow cylindrical conductors

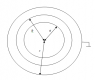
[gruba]

Homework Statement

Find potential and charge per unit length of every cylindrical hollow shell if the outer shell is grounded. The length is considered to be infinite.

Homework Equations

V=∫Edl

The Attempt at a Solution

I am not sure how to derive potentials for first two conductors (reference point is grounded third conductor). When integrating from (a to b)+(b to c) for the potential of the first conductor,
V₁=(λ₁/(2πε0))*(ln(b/a)+ln(c/b))
V₂=(λ₂/(2πε0))*ln(c/b)
Using superposition, charge per unit length of the third grounded conductor is
λ₃=λ₁+λ₂

Now, what I don't understand is that the conductors are hollow. This system of shells can't be looked as cylindrical capacitor, right? Could someone check my equations and show how to do this if it is not correct?

Thanks for replies.

 

[haruspex]

If $\lambda_1$ and $\lambda_2$ are positive, what will the sign of the charge on the grounded conductor be?

 

[gruba]

If $\lambda_1$ and $\lambda_2$ are positive, what will the sign of the charge on the grounded conductor be?

Ok, I solved the problem. Charge on the grounded charge will be negative.