Are These T-Test and Effect Size Calculations Correct?

[nobahar]

Hello! I hope it's okay to ask stats questions...
I think the calculations are correct, but I would appreciate it if someone could check for me!
These are the results from the exp. using repeated measures. My hypothesis is that the reuslts in condition 2 should be less than condition 1.
Cond 1
49
41
42
44
44
42
66
57
44
66
66
59
Cond 2
43
39
36
42
48
41
38
44
34
40
32
43

I know working out the standard deviation is tedious, but I checked with excel and it matched (I used n-1, so I got the population, not just the sample).
So, for condition 1:
mean=51.66666667
s.d.= 10.36895132
standard error= 2.99325842
and condition 2:
mean= 40
s.d.= 4.51260859854
standard error= 1.30267789
These (I think) are correct, its the t-test, p value and effect size I would greatly appreciate some feedback for.
For the t-test I used the realted t-test, since its repeated measures (same participant in both):

I got t= 3.346118674
are the units sd?
and DoF would be 11, and since I specified a direction, I got p=0.003261139 (one-tailed); which is significant? since P is less than 0.05?
and for effect size:

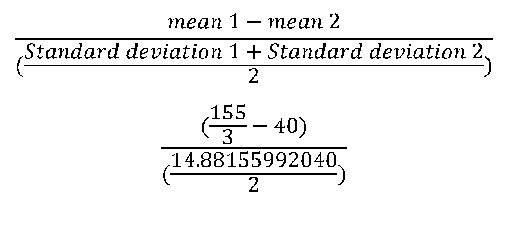
I got (d)= 1.567935986
Can somone verify the t-test, effect size and p value for me? Please! I used fractions at some points where I could quickly get the data (I wrote it down), in ideal circumstances should I use fractions for all the 'inputs' (e.g. stand. dev of difference, etc.), if possible, since its more 'accurate'?
Thanks! I now it's a lot to ask, but I would geratly appreciate it! I realize the formuale are slightly different depending on the narue of the experiment, I think I chose the right ones!

 

[Mark44]

It's been a while since I've done anything with statistics, but I think you might not be using the right form for t. The form I've included is for a two-sample t test, which seems to me the right one for your problem.

Instead of the standard error, I think you might need to use a pooled standard deviation.

t = \frac{X - Y}{S_p\sqrt{\frac{1}{12} + \frac{1}{12}}}
where X and Y are the sample means for the two conditions, and S_p is the pooled s.d., which is given as
\sqrt{\frac{(n - 1)s_x^2 + (m - 1)s_y^2}{n + m - 2}}
For your problem, n = m = 12.

Your use of fractions and decimal values probably won't affect your values, since you apparently used quite a few decimal places in your calculations.

The t distribution is close to a normal distribution with mean 0 and s.d. 1. For n around 30 there's no difference between the two distributions. That should answer your question about units of s.d.s.

Hope this is helpful.

 

[nobahar]

Thanks for the response!
I've got to do some reading... I haven't come across (or I don't think I have) the pooled s.d. yet.
I kow the related and independent t-tests. The latter being the (mean 1 - mean 2)/sqrt{(variance 1/n1)+(variance 2/n2)}.