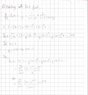Taylor Series using Geometric Series and Power Series

[jegues]

Homework Statement

See figure attached.

Homework Equations

The Attempt at a Solution

Okay I think I handled the lnx portion of the function okay(see other figure attached), but I'm having from troubles with the,

$$\frac{1}{x^{2}}$$

$$\int x^{-2} = \frac{-1}{x} + C$$

How do I deal with the C?

If I can get,

$$\frac{-1}{x}$$

I can work with it to get something like the following,

$$\frac{\text{first term of geometric series}}{1 - \text{common ratio}}$$

So what do I do about the C? Once I figure this out I can make more of an attempt into shaping,

$$\frac{-1}{x}$$

into the form mentioned above.

Any ideas?

Thanks again!

 

[vela]

You're going about it backwards. Use

$$\frac{1}{x^2} = -\frac{d}{dx}\left(\frac{1}{x}\right)$$

 

[jegues]

You're going about it backwards. Use

$$\frac{1}{x^2} = -\frac{d}{dx}\left(\frac{1}{x}\right)$$

Alrighty I think I've got a series for,

$$\frac{1}{x^{2}}$$

See figure attached. Is this correct?

I can't seem to figure out how to express it sigma notation however.

Any ideas?

 

[vela]

No, it looks like you integrated the series, but you want to differentiate -1/x to get 1/x².

 

[jegues]

No, it looks like you integrated the series, but you want to differentiate -1/x to get 1/x².

Whoops!

How does this look? (See figure attached)

 

[vela]

Looks good!