- #1
Redfire66
- 36
- 0
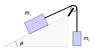
So I've been thinking about something for some time now, suppose you have an object (m1) on a frictionless ramp. There is an ideal pulley where the object is attached to one another and hangs down off the ramp (m2). And suppose that someone is holding the first block in place (m1) . If the person stops holding onto it, the first block will be pulled by the second block (hence m2 > m1).
I heard that the tension should be less than before
From what I assume, the net force on the first object should be greater than the net force on the second object (to keep it in place, however they should not equal each other right? Since that could mean there is a velocity)
Anyhow, if the tension of the rope is affected by the second object pulling on it (m2) then shouldn't the tension be the same since releasing the object doesn't change the tension applied from the block pulling on it?
I have a diagram here, I assume that the tension on block 1 should be the same on block 2.
I heard that the tension should be less than before
From what I assume, the net force on the first object should be greater than the net force on the second object (to keep it in place, however they should not equal each other right? Since that could mean there is a velocity)
Anyhow, if the tension of the rope is affected by the second object pulling on it (m2) then shouldn't the tension be the same since releasing the object doesn't change the tension applied from the block pulling on it?
I have a diagram here, I assume that the tension on block 1 should be the same on block 2.