Tension on a string between two masses.

[thatguythere]

Homework Statement

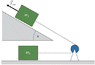
The figure below shows an object of mass m1 = 1.1 kg on an inclined surface. The angle of the inclined surface is θ = 31° with the horizontal. The object m1 is connected to a second object of mass m2 = 6.10 kg on a horizontal surface below an overhang that is formed by the inclined surface. Further, an external force of magnitude Fext = 14 N is exerted on the object with mass m1. We observe both objects accelerate. Assuming the surfaces and the pulley are frictionless, and the pulley and the connecting string are massless, what is the tension in the string connecting the two objects?

Homework Equations

F=ma

The Attempt at a Solution

I would simply like someone to verify my free body diagrams, so that I know whether I am working with the proper forces or not. Also, does the normal force and the perpendicular force cancel out?

 

[PhanthomJay]

Your 2nd FBD is good. But not so on the first. You are missing the tension force, and what you are calling f_perp and f_parallel are the components of mg, which replace mg in your diagram.

 

[thatguythere]

So in this case, is F_parallel even applicable since the mass seems to be in equilibrium prior to the exerted force causing it to accelerate?

 

[PhanthomJay]

So in this case, is F_parallel even applicable since the mass seems to be in equilibrium prior to the exerted force causing it to accelerate?

no, that is not correct, without the applied force, the block would slide down the plane and the string would go slack . But anyway, it is given that an external force is applied and the system is accelerating, so you must identify forces for that loading case.

 

[thatguythere]

So the forces acting upon m1 are f_ext = 14cos31 = 12.00
f_parallel = mgsin31 = 5.55
T = ?
And upon m2 T = ?
On m1 the normal force and perpendicular cancel out, as well the F_g and F_n on m2?

 

[SarahBB]

How did you figure this out? I have a similar problem and I am having issues figuring it out any help would be appreciated.

 

[thatguythere]

I just cannot seem to find the proper forces on m1. I would think that I would end up with something like. For mass 1 Fx-T = 1.1a and for mass 2 T = 6.1a
Fx - (6.1a) = 1.1a
Fx = 7.2a
a = Fx/7.2

T = 6.1a

 

[PhanthomJay]

So the forces acting upon m1 are f_ext = 14cos31 = 12.00

You should choose the x-axis parallel to the incline and the y-axis perpendicular to the incline. In this manner, f_ext is 14 up the plane.

f_parallel = mgsin31 = 5.55

yes, down the plane.

T = ?

yes, T is still unknown at this point, and the sum of all these forces is equal to what, per Newton 2?

And upon m2 T = ?[

T = what , per Newton 2?

On m1 the normal force and perpendicular cancel out, as well the F_g and F_n on m2?

yes, why?

 

[thatguythere]

Victory!

 

[PhanthomJay]

Victory!

Sweet!