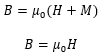The forum discussion focuses on the relationship between temperature (K) and magnetism (mT), specifically how temperature affects the magnetic properties of materials. It highlights that as temperature increases, particularly to the Curie point (1417°F for iron), the magnetic dipoles within materials become disordered, leading to a loss of magnetism. The discussion also addresses the linear and non-linear relationships between magnetization (M) and magnetic field (B), emphasizing that ferromagnetic materials can exhibit saturation and negative susceptibility under certain conditions.
PREREQUISITESPhysicists, materials scientists, and engineers interested in magnetism, as well as students conducting experiments related to temperature effects on magnetic properties.
zac_physics_student said:
Your question of the linearity is quite interesting. In general, the ## M ## in the material responds to the ## B ## in the material, most often in a linear fashion, but in ferromagnetic materials it can reach a saturation point. For linear materials, and really in general, we can always write ## M=\chi' B ## for some ## \chi' ##, where ## \chi' ## may have some ## B ## dependence for large ## B ##. Since we can also write ## B=\mu_o H+M ## , substituting in ## B=M/\chi' ## gives ## M=\mu_o H \frac{\chi'}{1-\chi' } ##. ## \\ ## In many materials, ## \chi '<< 1 ## so that it is straightforward to write ## M=\chi \, \mu_o H ## where ## \chi=\frac{\chi'}{1-\chi'} ##. ## \\ ## When ## \chi' > 1 ##, as it can be in the case of a ferromagnetic material, ## \chi ## becomes negative, and although we can still write ## M=\chi \, \mu_o H ## for this number ## \chi ##, the number ## \chi ## needs to be found from a hysteresis graph of ## M ## vs. ## H ##. In the case of a permanent magnet, the operating point is in the first or 4th quadrant of the hysteresis curve where ## M ## is opposite the direction of ## H ## and ## \chi ## is negative. Notice the constant ## \chi' ## is actually much better behaved than ## \chi ## in that ## M ## and ## B ## will always point in the same direction for paramagnetic and ferromagnetic materials. (Note: For paramagnetic and ferromagnetic materials ## \chi'>0 ##. For diamagnetic materials, ## \chi'<0 ## ). ## \\ ## For additional details, see also the following Insights article: https://www.physicsforums.com/insights/permanent-magnets-ferromagnetism-magnetic-surface-currents/ (c.g.s. units are used in the article, but the results can be readily converted to M.K.S.). ## \\ ## One additional question you may have is, why the odd behavior for the response of the ## M ## to ## H ##? The answer is ## H ## is not in general a magnetic field. Although it can be partly composed of magnetic fields, in the material the ## H ## from its own poles represents a correction term to the ## B ## from the magnetic surface currents that differs from ## M ## for geometries other than a long cylinder.(And that explains why ## \chi ## is negative in the permanent magnet. This ## H ## in the material from its own magnetic poles (that occur as a result of the magnetization ## M ## ) is simply a correction term to the magnetic field ## B ## which forr a long cylindical geometry has ## B=M ## that arises from the magnetic surface currents from the magnetization ## M ##.) ## \\ ## The magnetic field inside a permanent magnet is ## B=M ## along with the correction term ## \mu_o H ## computed from its own poles which points in the opposite direction. This is one of a couple of reasons why we have the equation ## B=\mu_o H+M ##. In addition to ## H ## from its own poles, ## H ## also consists of contributions from magnetic poles external to the material, as well as from any currents from conductors where it is computed via Biot-Savart's law. ## \\ ## In the case of a sample of material inside a current-carry solenoid, the applied ## B_a=\mu_o H_a ## where ## H_a ## is from the solenoid, but this scenario where this ## H_a ## is treated as the magnetic field ignores the internal ## B=M ## from the magnetic surface currents that result from the magnetization of the material. The applied field is ## B_a=\mu_o H_a ##, and this is what the hysteresis curve ## M ## vs. ## H_a ## uses, but the actual magnetic field in the material is ## B=\mu_o H_a+M ##. (Besides the hysteresis curve of ## M ## vs. ## H_a ##, it could also be useful at times to have a graph of ## M ## vs. ## B ##). ## \\ ## In summary, ## B ## is the actual magnetic field, and ## H ## is actually something of a mathematical construction.zac_physics_student said: