seto6
- 248
- 0
part 2 The Electric Field of a Continuous Distribution of Charge
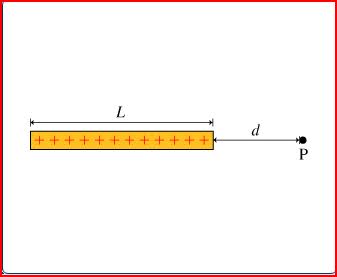
find the electric potential at point p
v=Kq/r...v=Er.
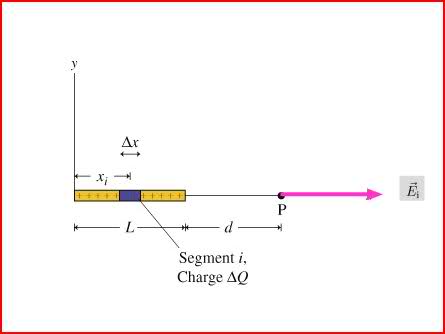
using this pic above and dQ=(Q/L)(dX)
v=(K)(dQ)/(L-(X_i)+d) then sub dq=dX(Q/L)
we get...
(KQ/(L))(dX/(L+d-(X_i)) then integrating
V=(KQ/L)((-ln(d))+(ln(L+d)))
is this correct? if not could some one tell me where i went wrong.
thanks in advance.
Homework Statement
find the electric potential at point p
Homework Equations
v=Kq/r...v=Er.
The Attempt at a Solution
using this pic above and dQ=(Q/L)(dX)
v=(K)(dQ)/(L-(X_i)+d) then sub dq=dX(Q/L)
we get...
(KQ/(L))(dX/(L+d-(X_i)) then integrating
V=(KQ/L)((-ln(d))+(ln(L+d)))
is this correct? if not could some one tell me where i went wrong.
thanks in advance.
Last edited: