The jumping skier (momentum, Newton's laws, energy)

[pinsky]

Homework Statement

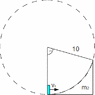
So, there is a skier (the blue recktangle) preparing to do a jump. There is no friction between the skier and the jumping board, and also no friction between the jumping board and the ground.

Known values are:

v0 - starting speed of the skier
m2 - mas of the jumping board
m1 - mass of the skier
radius and angle (as shown)

The circle is just to show that the jumping board has a form o a circle arc.

I need to find the speed of the skier at the moment when he leaves the jumpingboard (or jumps), and the angle of the speed.

Homework Equations

G=m*v
F=m*a
V=v0 + integral{a(t) dt}

?

The Attempt at a Solution

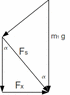
F_s is the perpendicular force the skier is applying to the jumping-board. It changes with the angle. Alpha is the current angle of the tangent (it's actually a decomposition of the jumping board to triangle like slopes).

I'm basically blocked. I've done the vector decomposition, but i can't set the equations. I'm sure there should be some differentiation here, but i just don't know what.

Some ideas? No need to write formulas, just the starting idea?

Thanx

 

[tiny-tim]

hi pinsky!

Known values are:

v0 - starting speed of the skier
m2 - mas of the jumping board
m1 - mass of the skier
radius and angle (as shown)
…
I need to find the speed of the skier at the moment when he leaves the jumpingboard (or jumps), and the angle of the speed.

no, this has nothing to do with vectors or with force

this is a straightforward conservation of energy problem …

start again ​

 

[pinsky]

Got it!

Thanks!

But, the way with Newtons laws is also possible if we use differentiation, it just way more complicated?

(i like to at least have the idea of other solutions)

 

[tiny-tim]

yeees … you could find the force at each position, and then do a complicated differential equation …

eugh!​

 

[pinsky]

In the example i needed help with, the jumping board was not fixed in place, but had a finite mass. Let's call that velocity v2. It will have an angle different from 45° if observed from an external coordinate system.
Or, the velocity will have an angle 45° if we observe it from the jumping board coordinate system


In the first example of this problem (one which i didn't mention) the jumping board was stationary, and i also had to calculate the velocity of the skier when he leaves the jumping board.


That was easily calculated through one "preservation of energy" equation for the skier. Let's call that speed v1. Since both external and jumping boards coordinate systems are equal, the angle was always 45°.


What i can't figure out now is, is the velocity of the skier in the second example (when the jumping board is movable), when observed through the coordinate system of the board, equal as the one in the first example?

If yes/no why?

Trying to build up some intuition here :)

 

[tiny-tim]

hi pinsky!

can you please clarify what the jumping board is?

in the diagram, is it that almost-triangle with "m₂" in the middle, and does it slide along the ground?

 

[pinsky]

Yes, it is the almost triangle and it slides along the ground without friction. :)

 

[tiny-tim]

hi pinsky!

What i can't figure out now is, is the velocity of the skier in the second example (when the jumping board is movable), when observed through the coordinate system of the board, equal as the one in the first example?

If yes/no why?

but the board is accelerating, so you can't find a convenient coordinate system based on the board

you'll have to use conservation of energy and conservation of momentum