A The k direction in a k.p model ?

[lichen1983312]

I am trying to do some calculation based on a k.p model of GaN proposed by S. Chuang [Phys. Rev. B, 54, 2491]. It is a 8 by 8 Kane model with basis functions:

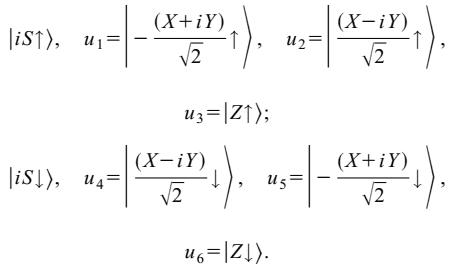
The 8 by 8 Hamiltonian contain first order of k is

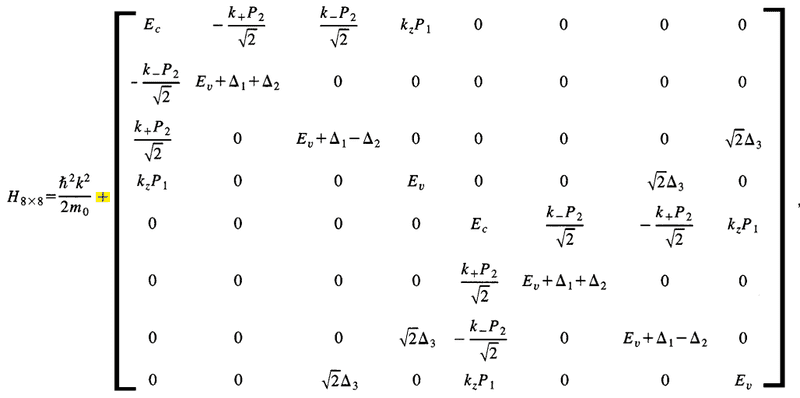
where ${k_ \pm } = {k_x} \pm i{k_y}$

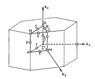
the reciprocal space and high symmetry points is pictures as [Phys. rev. B, 53, 10173]

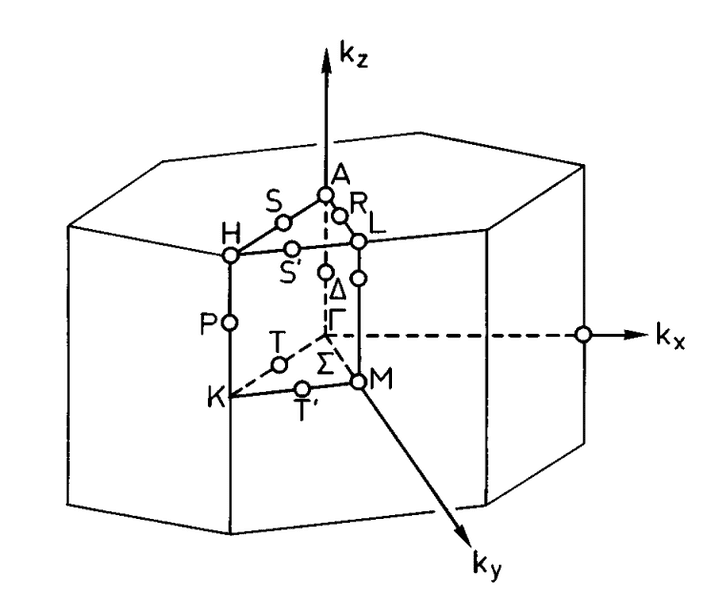
My question is: How is the direction of kx and ky defined in the 8 by 8 Hamiltonian?
Put is in another way. If I want to draw a E-k curve along $\Gamma \to M$, how do I express this direction in terms of kx and ky ?
Thanks very much, please help.

 

[DrDu]

$k=(0,\lambda,0)^T$ with $\lambda=0$ corresponding to $\Gamma$ and $\lambda=k_\mathrm{M}$ corresponding to M?

 

[lichen1983312]

$k=(0,\lambda,0)^T$ with $\lambda=0$ corresponding to $\Gamma$ and $\lambda=k_\mathrm{M}$ corresponding to M?

Thanks
That is what is said in the graph, which is taken from a different article.

But if I only look at the Hamitonian and the basis functions, how can I tell?

 

[DrDu]

$\Gamma$, M , $\Sigma$, means that the hamiltonian is invariant under a specific group of rotations and reflections, respectively, which also leave k invariant. These groups are called the "little groups of the wavevector". This are sub groups of the point group under which $\Gamma$ is invariant. Look up which elements they contain in case of the Point Group of GaN and make sure that for the coice of k, your Hamiltonian is invariant under the corresponding transformations.

 

[lichen1983312]

$\Gamma$, M , $\Sigma$, means that the hamiltonian is invariant under a specific group of rotations and reflections, respectively, which also leave k invariant. These groups are called the "little groups of the wavevector". This are sub groups of the point group under which $\Gamma$ is invariant. Look up which elements they contain in case of the Point Group of GaN and make sure that for the coice of k, your Hamiltonian is invariant under the corresponding transformations.

Thanks very much, I will look into it.