- #1
nishantve1
- 76
- 1
So I have been dealing with the modulus function for almost a year now , I didn't ran into it many times so didn't really tried to understand it well . But it has started to get a little bit confusing . So if someone helps me I will be really happy .
From what I know
f(x) = |x| = { x ; x >= 0 and -x ;x<=0
That means |-5| = 5 and |5| = 5
And it has a graph
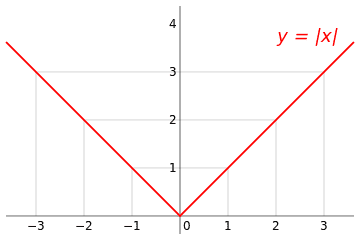
But this does not satisfy my intuition , for me the function and the graph says two different thing , I mean the function says
f(x) = |x| = {-x ;x<=0
so if I plug in -5 which is less than 0 then the output should be -5 only
I know I am wrong but I am just going with function definition . What does the definition actually say ?
Also I encounter problems while sketching graphs of the mod function .
If someone can help me with the graph of
f(x) = |1-x+|x|| it would be awesome
I can graph it using wolframalpha but I want to know how it came about
Thanks
From what I know
f(x) = |x| = { x ; x >= 0 and -x ;x<=0
That means |-5| = 5 and |5| = 5
And it has a graph
But this does not satisfy my intuition , for me the function and the graph says two different thing , I mean the function says
f(x) = |x| = {-x ;x<=0
so if I plug in -5 which is less than 0 then the output should be -5 only
I know I am wrong but I am just going with function definition . What does the definition actually say ?
Also I encounter problems while sketching graphs of the mod function .
If someone can help me with the graph of
f(x) = |1-x+|x|| it would be awesome
I can graph it using wolframalpha but I want to know how it came about
Thanks