baby_1
- 159
- 16
As you can see in this picture:
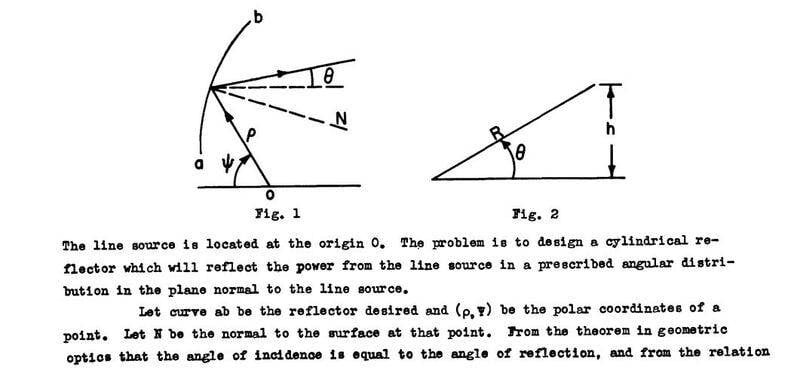 This explanation "relation between the normal and the slope of a curve" is formulated here:
This explanation "relation between the normal and the slope of a curve" is formulated here:
$$\frac{1}{\rho} \frac{d\rho }{d\psi }=\tan\left(\frac{\theta+\psi}{2}\right)$$
I got confused because I don't have the curve equation(regarding the slope of the curve and normal vector) and I am curious to know how the above equation is derived.
First I assume that the normal vector on cylindrical curve is going to obtain via gradian operator:
$$\bigtriangledown F=\frac{\partial F }{\partial r}\hat{ar}+\frac{\partial F }{r\partial \phi}\hat{\phi}+\frac{\partial F }{\partial z}\hat{az}$$
but I don't have the F function, and as you can see the above question the writer assume F as $$\rho$$ that I don't understand where it comes from and why the writer used the only phi component.
I will be grateful if you could help me to obtain the formula based on the curve coordinates.
$$\frac{1}{\rho} \frac{d\rho }{d\psi }=\tan\left(\frac{\theta+\psi}{2}\right)$$
I got confused because I don't have the curve equation(regarding the slope of the curve and normal vector) and I am curious to know how the above equation is derived.
First I assume that the normal vector on cylindrical curve is going to obtain via gradian operator:
$$\bigtriangledown F=\frac{\partial F }{\partial r}\hat{ar}+\frac{\partial F }{r\partial \phi}\hat{\phi}+\frac{\partial F }{\partial z}\hat{az}$$
but I don't have the F function, and as you can see the above question the writer assume F as $$\rho$$ that I don't understand where it comes from and why the writer used the only phi component.
I will be grateful if you could help me to obtain the formula based on the curve coordinates.
