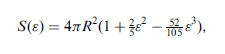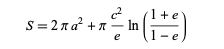Discussion Overview
The discussion revolves around the surface area of an oblate ellipsoid, specifically focusing on the discrepancies between a formula derived by a participant and one presented in a textbook. The scope includes mathematical reasoning and technical exploration of the definitions and calculations involved.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant expresses difficulty in matching their derived formula for the surface area of an oblate ellipsoid with the result from a textbook, despite using Taylor expansions.
- Another participant notes that the derived formula works through order zero but does not provide further clarification on the discrepancy.
- A participant presents their final result for the surface area, which includes terms up to ε^3, and indicates a significant difference from the textbook result.
- There is a discussion about the absence of a linear term in ε, attributed to the even nature of the function, prompting questions about the definition of R in the first approximation.
- Clarification is sought regarding the variable c in the participant's formula, with references to a similar formula from a professor that uses b instead of c.
- One participant suggests verifying the definitions of eccentricities and offers to help if the complete calculations are shared, indicating potential confusion over definitions used in the discussion.
Areas of Agreement / Disagreement
Participants express differing views on the definitions and calculations related to the surface area of the oblate ellipsoid. There is no consensus on the correct formula or the definitions of the variables involved.
Contextual Notes
Participants mention the need for clarity on definitions and the potential for discrepancies due to differing interpretations of variables like c and b. The discussion highlights unresolved mathematical steps and assumptions regarding the eccentricities.