Thermodynamics: ideal gas chemical potential pressure dependence

[alpha358]

I don‘t understand one step in derivation of ideal gas chemical potential.

Generally Gibbs free energy is:

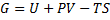(1)

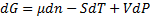(2)​

We observe that:

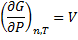(3)​

From equation (3) we make differential equation and integrate it:

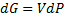(4)

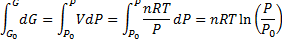(5)​

We get Gibbs free energy dependence on pressure:

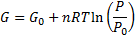(6)
​

Equation (6) is true strictly when:

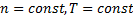, because of equation. (3).

Later we derive chemical potential for ideal gas:

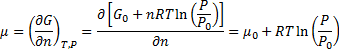(7)
​

Here we assumed that

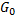is a function of n. (because it is an extensive property), therefore:

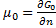
In the end we get pressure dependency of chemical potential for ideal gas:

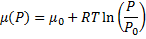(8)​

Note that in equation (7) we differentiate equation (6) by n and eq. 6 is derived only for condition when n = const and T = const.
In other words, we differentiate it with respect to variable which should stay constant.
Are we allowed to do this ?

 

[ZetaOfThree]

The short answer is yes. Even though $n$ is constant in taking the derivative $\left(\frac{\partial G}{\partial P} \right)_{n,T}$, the value of the derivative will depend on what value of $n$ you choose. For example if you had something like $y=nx$ then $\left(\frac{\partial y}{\partial x} \right)_{n}=n$. So even though $n$ is constant in taking the derivative, it still depends on $n$ and you can take its derivative again with respect to $n$.

 

[alpha358]

Thanks, now it seems so trivial :D

 

[Chestermiller]

The original equation you wrote down applies only to a system in which the total number of moles of gas is varying, while the composition of the gas is constant. In such a situation,

$G=n\mu(T,P)$

For situations in which the composition of the gas can also vary, see Smith and Van Ness, Introduction to Chemical Engineering Thermodynamics.

Chet

 

[DrDu]

The original equation you wrote down applies only to a system in which the total number of moles of gas is varying, while the composition of the gas is constant. In such a situation,

$G=n\mu(T,P)$

For situations in which the composition of the gas can also vary, see Smith and Van Ness, Introduction to Chemical Engineering Thermodynamics.

Chet

For an ideal gas, the variation of the composition can be taken into account by simply using the partial pressure throughout, as the different components of the gas don't interact, i.e. you don't have to consider the mixture effects at all in an ideal mixture.

 

[DrDu]

The original equation you wrote down applies only to a system in which the total number of moles of gas is varying, while the composition of the gas is constant. In such a situation,

$G=n\mu(T,P)$

For situations in which the composition of the gas can also vary, see Smith and Van Ness, Introduction to Chemical Engineering Thermodynamics.

Chet

For an ideal gas, the variation of the composition can be taken into account by simply using the partial pressure throughout, as the different components of the gas don't interact, i.e. you don't have to consider the mixture effects at all in an ideal mixture.

 

[Chestermiller]

For an ideal gas, the variation of the composition can be taken into account by simply using the partial pressure throughout, as the different components of the gas don't interact, i.e. you don't have to consider the mixture effects at all in an ideal mixture.

Yes. This is correct. The chemical potential of each species is as DrDu indicates. But, the derivation of why it works out this way requires some derivation, and Smith and Van Ness do a very nice job of providing this derivation (Chapter 10).

Chet