Andrew Pierce
- 8
- 0
Homework Statement
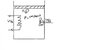
An insulated piston-cylinder device contains 5 L of saturated liquid water at a constant pressure of 175 kPa. Water is stirred by a paddle wheel while a current of 8 A flows for 45 min through a resistor placed in the water, If one-half of the liquid is evaporated during this constant pressure process and the paddle -wheel work amounts to 400 kJ, determine the voltage of the source. Also, show the process on a P-v diagram with respect to saturation lines.
Homework Equations
ΔE = Ein - Eout
Welectric = VIΔt
if ΔP = 0, ΔH = m(h2 - h1)
ΔH = ΔU + Wboundary
The Attempt at a Solution
V = 5 L
m = 5 kg (by conversion)
P = 175 kPa
I = 8 A
Δt = 45*60 sec = 2700
Assuming that KE, and PE = 0,
ΔE = ΔU
Also since it is insulated we are assuming that the heat lost is 0
We + Wsh - Wboundary = ΔU
We + Wsh = ΔU + Wboundary
We + Wsh = ΔH
We + Wsh = m(h2 - h1)
Here is where I get lost. I know that we can find h1 from the saturated water tables
h1 = 487.01 kj/kg (at Psat = 175 kPa)
I'm confused as to where the second enthalpy value comes from since our state has constant P.
Also the P-v should look something like this I believe: