Thermodynamics Proof : Cv (non-ideal gas) - Cv (ideal gas)

[Exploded_Muffin]

Can someone please help me with the following proof ...I'm stuck and not sure if I'm even on the right path.

Prove that

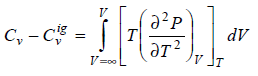What I've done so far;
if U = f(T,V)
dU = (∂U/∂T)v dT + (∂U/∂V)t dV

Cv (non ideal) = (∂U/∂T)v

Using dU = TdS - PdV and Maxwell relation (∂S/∂V)t =(∂P/∂T)v,
(∂U/∂V)t = T(∂P/∂T)v - P

So;
dU = CvdT + [ T(∂P/∂T)v - P ]dv

I'm basically stuck here, tried different ways forward from here but I can't seem to arrive at the correct answer. Any help would be

 

[Chestermiller]

This is a homework problem, so I am moving it to a homework forum.

You want to find U(T+dT, V) - U(T,V), where V is a small enough volume so that ideal gas behavior does not to apply. What you do is start at T,V and determine the isothermal change in U when you go from T,V to very large volume (infinite). This puts you in the ideal gas region. Then you take the change in U from T and infinite volume to T + dT and infinite volume. This is just the ideal gas heat capacity times dT. Then you go isothermally from T+dT and infinite volume to T+dT and finite volume V.

Chet