Adesh
- 735
- 191
- Homework Statement
- See the main body.
- Relevant Equations
- We don’t need them.
These are the images from Sommerfeld’s Lectures on Theoretical Physics, Vol 2 chapter 2, section 6, Equilibrium of Incompressible Fluids.

Image 1
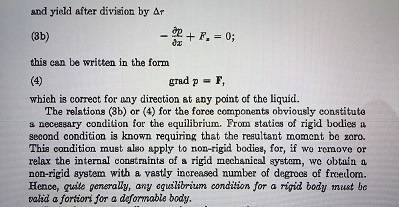
Image 2
Doubt 1 : What does it mean for a force to act on a fluid volume? Force acts on a point, force may act on a surface but I’m unable to understand what it means “external force per unit of fluid volume”. Did Sommerfeld mean that ##\mathbf F## acts on all six faces of that fluid volume element ?
Doubt 2 : I really couldn’t understand what happened after equation 3a. Why we divided by ##\Delta \tau## and how ##F_x## came in equation 3b ?
Doubt 3 : How equation 3b and 4 “obviously” constitute a necessary condition for the equilibrium? I’m unable to understand how ##grad~ p = \mathbf F## is a necessary condition for the equilibrium.
Please explain the above said doubts to me, if my question is too broad please let me know.
Thank you.
Image 1
Image 2
Doubt 1 : What does it mean for a force to act on a fluid volume? Force acts on a point, force may act on a surface but I’m unable to understand what it means “external force per unit of fluid volume”. Did Sommerfeld mean that ##\mathbf F## acts on all six faces of that fluid volume element ?
Doubt 2 : I really couldn’t understand what happened after equation 3a. Why we divided by ##\Delta \tau## and how ##F_x## came in equation 3b ?
Doubt 3 : How equation 3b and 4 “obviously” constitute a necessary condition for the equilibrium? I’m unable to understand how ##grad~ p = \mathbf F## is a necessary condition for the equilibrium.
Please explain the above said doubts to me, if my question is too broad please let me know.
Thank you.
Last edited by a moderator: