Time Dilation: Explaining Light Speed Travelers

[clnotx]

I was hoping someone could explain to me how if someone travels to a distant point in space at the speed of light and then comes back traveling at this speed, how would the people still here on Earth have aged more than the person that traveled at the speed of light? Thanks

 

[Crosson]

Your question is a "How?" and physicists generally prefer to deal with "what?".

Think about spacetime, as one thing. We all move through spacetime at the speed of light, always (which is reduntant, because "always" mean "at all times").

When you are not moving in space, you are traveling purely in the time direction of space time. This means that standing still means time goes at its fastest rate.

If you start moving (through space), your space velocity and your time velocity must still together add up to the speed of light, so your time velocity must become smaller. This is the reason for the effect you describe.

 

[The Bob]

This is very much to do with Time Dilation and The Twin Paradox.

I am afraid I cannot find my papers on the subject and it has been about a year since I last looked at it, however, I have found some websites:

http://members.tripod.com/wmhxbigguy/Theory/time.html
http://www.walter-fendt.de/ph11e/timedilation.htm
http://www.phys.unsw.edu.au/~jw/time.html

The Bob (2004 ©)

 

[JesseM]

Your question is a "How?" and physicists generally prefer to deal with "what?".

Think about spacetime, as one thing. We all move through spacetime at the speed of light, always (which is reduntant, because "always" mean "at all times").

When you are not moving in space, you are traveling purely in the time direction of space time. This means that standing still means time goes at its fastest rate.

If you start moving (through space), your space velocity and your time velocity must still together add up to the speed of light, so your time velocity must become smaller. This is the reason for the effect you describe.

As I argued on this thread, I think this is actually a pretty poor description of what relativity is all about, since mainstream physics textbooks generally do not discuss the notion of "speed through spacetime" at all, and the way you are forced to define the words "speed through spacetime" to make this argument work is extremely counterintuitive.

A better way to understand time dilation, IMO, is just to understand it as a consequence of the fact that every reference frame must measure light to have the same speed--see the http://www.kineticbooks.com/physics/17467/17486/sp.html .

 

[Phobos]

Welcome to Physics Forums, clnotx!

To help clarify the above responses...

Einstein and others demonstrated that there is no absolute clock on the universe that everyone can agree on. Time passes for different people/things at different rates depending on that person's/thing's speed through space. It's called Time Dilation. It seems that space and time are closely linked and your movement through space affects your movement through time.

Consider someone who leaves Earth in a fast-moving rocket and someone who stays at home. Each will feel time proceed normally for themselves, but they will see the other person's clock proceed at a different rate (and it's not a problem with the clock...it's an actual effect on Time itself). The faster one goes compared to the other, the greater the Time Dilation.

It sounds illogical, but it has been verified experimentally.

The person on Earth will see the astronaut's time move slower, so the astronaut will age slower compared to people back on Earth.

It gets a lot more complicated as you explore this idea further, but that's a good start for the idea.

I'm going to move this discussion to the Relativity forum for further discussion.

 

[yogi]

As usual - I will take issue with Jesse and side with Crosson on the easy way to visualize the spacetime journey - you can get the correct answer in many ways - some of the ways are equivalent - others are not - but to avoid introducing more math than one might be comfortable with, the description set out by Brian Green (as well as Epstein and Hawking) serves as a good introductory framework.

The only caveat is that it could easily be inferred that one must start with a preferred reference frame that has no velocity with respect to the universe. And in adding the space velocity to the time velocity, you use the square root of the sum of the squares since the time axis is orthogonal to the space axis.

 

[JesseM]

As usual - I will take issue with Jesse and side with Crosson on the easy way to visualize the spacetime journey - you can get the correct answer in many ways - some of the ways are equivalent - others are not - but to avoid introducing more math than one might be comfortable with, the description set out by Brian Green (as well as Epstein and Hawking) serves as a good introductory framework.

The book about Hawking's work you mentioned on that thread was not written by Hawking, and looking back on that thread, you didn't even seem to remember whether the author was claiming that Hawking had used this particular argument, or whether it was just her own way of summarizing relativity. And do you really think it makes sense to define "speed through spacetime" as c d\tau / d\tau? Since d\tau / d\tau is obviously 1, doesn't this make the statement "everything moves through spacetime at the speed of light" pretty trivial, just a consequence of this odd definition rather than an interesting fact about the physical world? If you're going to use that term at all, wouldn't it make more sense to define it as ds/dt, where ds is the spacetime interval, a measure of "distance" in spacetime, so that "speed through spacetime" has the form of "spacetime distance/time"? If you can justify this stuff and explain why it makes sense to define the terms this way, I'm all ears.

 

[Crosson]

The speed through time is defined by:

\Frac{dt}/{d\tau}

The proper time is that of the observer, the time t is that of the observed. This quantity should be interpreted as "How much time does that guy go through when I go through one second?".

It is very sensible and not counter intuitive at all. Also, for those of you thinking I am singling out a preferred reference frame, the full blown statement looks like this:

"Everything in spacetime is moving at the speed of light, relative to everything else." So you are moving at c through spacetime relative to me, and I am moving at c through spacetime relative to you.

The reason this is not discussed in mainstream physics texts is that the 4-momentum is preferred to the 4-velocity. This is because velocity becomes counterintuitive in SR, as you have pointed out.

 

[JesseM]

The speed through time is defined by:

\Frac{dt}/{d\tau}

The proper time is that of the observer, the time t is that of the observed. This quantity should be interpreted as "How much time does that guy go through when I go through one second?".

It is very sensible and not counter intuitive at all.

I agree that this definition of "speed through time" is not too counter-intuitive, but what I was calling counterintuitive was the way "speed through spacetime" must be defined in order to make the argument work. If you define "speed through spacetime" as the magnitude of the 4-velocity vector u = (cdt / d\tau, dx / d\tau, dy / d\tau, dz / d\tau), this works out to \sqrt{c^2 dt^2 - dx^2 - dy^2 - dz^2 }/d\tau = c\sqrt{dt^2 - c^{-2}(dx^2 + dy^2 + dz^2)} / d\tau = cd\tau / d\tau. To me, it does not make much sense to define "speed through spacetime" as cd\tau / d\tau, and the statement that "everything moves through spacetime at the speed of light" seems to be just a trivial consequence of this weird definition, not an interesting statement about the physical world.

 

[robphy]

Something bothers me about this "speed through time"... but I can't put my finger on it until I get some clarifications.

I don't have the Elegant Universe... I'm only going on JesseM transcription in
https://www.physicsforums.com/showpost.php?p=430613&postcount=3 and the recent posts in this thread.
Is this transcription accurate?
Specifically, (in my reconstruction of the quote)

Now, we can rearrange the equation c^2(dt/d\tau)^2 - (d\vec{x}/d\tau)^2 = c^2, to be c^2(d\tau/dt)^2 + (d\vec{x}/dt)^2 = c^2. This shows that an increase in the object's speed through space, \sqrt{(d\vec{x}/dt)^2} must be accompanied by a decrease in d\tau/dt, the latter being the object's speed through time (the rate at which time elapses on its own clock, d\tau, as compared with that on our stationary clock, dt).

I ask because the use of "speed through time" in the transcription (from above: d\tau/dt) is different from recent posts (below: \Frac{dt}/{d\tau}) is different

The speed through time is defined by:
\Frac{dt}/{d\tau}
The proper time is that of the observer, the time t is that of the observed. This quantity should be interpreted as "How much time does that guy go through when I go through one second?".

I agree that this definition of "speed through time" is not too counter-intuitive, but what I was calling counterintuitive was the way "speed through spacetime" must be defined in order to make the argument work. If you define "speed through spacetime" as the magnitude of the 4-velocity vector...

Can someone clarify?
Can someone draw a spacetime diagram?

 

[JesseM]

robphy, I just rechecked The Elegant Universe and confirmed that Greene does define "speed through time" as d\tau / dt.

 

[yogi]

Jesse - the Hawking reference was Kitty Fergeson's book - it was based upon interviews with Hawking and he approved the contents - this was one of the early books written in conjuction with Hawking. It is the least mathematical way of explaining the spacetime interrelationship - for that reason alone it should not be relegated to any lesser status that any of the other ways of getting relativistic ideas across. In fact it offers insight. Moreover it leads directly to the transforms for time dilation and length contraction w/o further hypothesis

 

[yogi]

Green attributes the idea to Einstein - I vaguely remember coming across it in one of his lesser known musings - but I have been unable to locate it - anybody want to email Brian Green and find out if Einstein really entertained that notion.

 

[JesseM]

Jesse - the Hawking reference was Kitty Fergeson's book - it was based upon interviews with Hawking and he approved the contents

But that doesn't necessarily mean he actually would explain relativity that way, maybe he just that he had no objection to Fergeson explaining it that way. And like I said, the explanation is certainly correct mathematically, I'm more objecting to the use of terminology on pedagogical grounds.

It is the least mathematical way of explaining the spacetime interrelationship

Is it? What if I just said, "the faster your speed, the slower your clocks will run"--what would this explanation lack that the "greater speed through space means less speed through time, because speed through spacetime must be c" explanation doesn't?

Moreover it leads directly to the transforms for time dilation and length contraction w/o further hypothesis

Not unless you give more mathematical details about it, like Greene did in his footnote. For example, just from the verbal description you might think it was saying that d\tau /dt + d\vec{x}/dt = c, or cd\tau /dt + d\vec{x}/dt = c if you noticed that the units of each term had to be the same, but this would be incorrect, it's actually c^2(d\tau/dt)^2 + (d\vec{x}/dt)^2 = c^2

Green attributes the idea to Einstein

What he says is "Here's the leap: Einstein proclaimed that all objects in the universe are always traveling through spacetime at a fixed speed--that of light." I interpreted this as just paraphrasing the idea that the magnitude of the 4-velocity is always c according to Einstein's theory of relativity, not necessarily saying that Einstein ever called this magnitude "the speed through spacetime".

By the way, it's "Greene", not "Green".

 

[robphy]

Here's my $0.02 on the "speed through time" and "speed through spacetime" idea (based on my understanding of the transciption of a small passage from the Elegant Universe). (In short, I think my comments below are an elaboration of JesseM's position.)

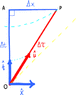
To me, "speed through spacetime" means the "spacetime-norm of an object's 4-velocity". In relativity, the 4-velocity of an observer is the unit tangent-vector to the observer's worldline. In the attached diagram, it is the Minkowski-unit vectors \hat t and \hat u shown.

Since, by convention, time is measured in seconds and space in meters, one has to multiply the time-components by a speed, (say) "the speed of light" [that is, the spatial-speed of a light ray], in order to work with spacetime components with homogeneous units. Any speed could have been used to make the units homogeneous. In special relativity, it is convenient to use the "speed of light" to avoid the nuisance of carrying around a dimensionless factor.

Now here are some reasons why emphasizing the "speed through spacetime" idea doesn't seem that useful to me.

[As someone must have mentioned before] In special relativity, the "speed through spacetime" of a light ray is ZERO... since light rays have lightlike or "null" tangent-vectors. While certainly true, I wonder if this might be more confusing to a beginner.

Secondly, if one were to formulate a spacetime geometry for Galilean Relativity, one would also normalize 4-velocities as described above. To work with homogeneous units, one would still have to use a speed. Of course, the speed of light wouldn't be anything special in Galilean Relativity. But let's use it (or, if you wish, any other speed playing the role of a conversion unit). One would still say that all observers travel with that same "speed through spacetime". So, the phrase seems rather empty...except to say that "an observer's 4-velocity is a unit vector (in the appropriate spacetime geometry)".

Now, concerning "speed through time"...

If "speed through space" is \displaystyle \frac{dx}{dt} (the rate of change of the object's-spatial-displacement with respect to the object's-time-displacement, \displaystyle\frac{(PA)}{(AO)}=\frac{\sinh\theta}{\cosh\theta}=\tanh\theta, (where \theta is the rapidity), then, by analogy, "speed through time" is \displaystyle \frac{dt}{dt} (the rate of change of the object's-time-displacement with respect to the object's-time-displacement, \displaystyle\frac{(AO)}{(AO)}=1).

Thus, it would seem inappropriate to use "speed through time" to mean \displaystyle <br /> \frac{d\tau}{dt} (the rate of change of the object's-proper-time-displacement with respect to the object's-time-displacement, \displaystyle\frac{(PO)}{(AO)}=\frac{1}{\gamma}=\frac{1}{\cosh\theta}).
"speed through proper-time" might be more appropriate.


Finally, it might be interesting to express the following relations in terms of the rapidity
\theta:

<br /> \begin{align*}<br /> c^2\left(dt/d\tau\right)^2 - \left(d\vec{x}/d\tau\right)^2 &amp;= c^2\\<br /> c^2\left(\displaystyle\frac{(AO)}{(PO)}\right)^2 - \left(c\displaystyle\frac{(PA)}{(PO)}\right)^2 &amp;=\\<br /> c^2(\cosh\theta)^2 - c^2(\sinh\theta)^2 &amp;=\\<br /> \end{align*}<br />

and

<br /> \begin{align*}<br /> c^2\left(d\tau/dt\right)^2 + \left(d\vec{x}/dt\right)^2 &amp;= c^2\\<br /> c^2\left(\displaystyle\frac{(PO)}{(AO)}\right)^2 + \left(c\displaystyle\frac{(PA)}{(AO)}\right)^2 &amp;=\\<br /> c^2\left(\displaystyle\frac{1}{\cosh\theta}\right)^2 + c^2(\tanh\theta)^2 &amp;=\\<br /> c^2\left(\displaystyle\frac{1}{\cosh\theta}\right)^2 + <br /> c^2\left(\displaystyle\frac{\sinh\theta}{\cosh\theta}\right)^2 &amp;=\\<br /> c^2\left(\displaystyle\frac{1+\sinh^2\theta}{\cosh^2\theta}\right) &amp;=<br /> \end{align*}<br />

Note:
In the first expression, it's the usual difference of the square-norms of the Minkowski-perpendicular legs of this triangle. (The signature of the metric is evident here.)
In the second expression (which may appear to look Euclidean at first glance), it is effectively the sum of the square-norms of the timelike-hypotenuse (PO) and the spacelike-leg (PA). Note carefully that (PO) is not Minkowski-perpendicular to (PA).

In summary, the mathematics is, of course, correct.
However, the emphasis on "speed through spacetime" seems empty,
and the use of "speed through time" seems inappropriate since it involves the proper-time of the object along (OP).

Maybe I should get myself a copy of the Elegant Universe to see this passage for myself... in case I've misunderstood the transcription.

 

[Mortimer]

The expression d\tau/dt as used in Brian Greene's book is the expression for velocity through time in Euclidean relativity. Or more precise, it actually is cd\tau/dt. See posts number 33 and further in thread Spacetime intervals again - still figuring...
It is also explained with diagrams in this page: http://www.rfjvanlinden171.freeler.nl/4vectors. The page uses ds/dt for the (Euclidean) velocity in the time dimenson but, since ds=cd\tau, this leads to the expression as mentioned above.
Strictly spoken the expression cd\tau/dt does not represent a velocity. It represents c times the ratio of two velocities: the velocity in time of the moving object and the velocity in time of the observer at rest.
The independent expression for each individual velocity would require an extra parameter K (or dimension K, sorry to say it again, JesseM but it seems appropriate in this thread), leading to d\tau/dK, respectively dt/dK. The ratio then is
\frac{d\tau/dK}{dt/dK}
If K is chosen such that dt/dK=1 (the observers velocity in the time dimension is a constant) this leads to c\frac{d\tau}{dK} as a general expression for the velocity in the time dimension for moving objects.

 

[yogi]

Do you guys really think all the calculus and symbol manipulation is going to be simpler to a person who wants to get a grasp of the spacetime relationship.

Yes Jesse, I know its Greene - have his book here in front of me along with a lot of others written on the subject. Don't have all my references here however - so I am curious whether I ever really read that idea as originating from Einstein - if and when I come across it, you can bet I will let you know.

 

[Mortimer]

Do you guys really think all the calculus and symbol manipulation is going to be simpler to a person who wants to get a grasp of the spacetime relationship.

Well, if you want a really simple explanation (albeit based on Euclidean SR), look http://www.rfjvanlinden171.freeler.nl/simplified

 

[robphy]

Do you guys really think all the calculus and symbol manipulation is going to be simpler to a person who wants to get a grasp of the spacetime relationship.

Yes Jesse, I know its Greene - have his book here in front of me along with a lot of others written on the subject. Don't have all my references here however - so I am curious whether I ever really read that idea as originating from Einstein - if and when I come across it, you can bet I will let you know.

I don't know if your comment is partially directed to me.

In any case, the point of my analysis is to understand and verify the underlying physics and mathematics in an explanation given to beginners. The analysis is not meant for the beginner. If anything, it's meant to look out for the beginner.

 

[clnotx]

Im not sure about Green, but if your referring to Einstein making the original claim of traveling at the speed of light has a different effect of aging on the body, I came across this I believe in The Cosmos by Sagan. If this isn't what you were talking about please ignore. Also thanks to all for the help on my question.