Time period of oscillation of a physical pendulum and spinning disk

[Avi Nandi]

Homework Statement

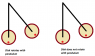
Find the period of a pendulum consisting of a disk of mass M and radius R fixed to the end of the rod of length l and mass m. How does the period change if the disk is mounted to the rod by a friction less bearing so that it is perfectly free to spin? The centre of the disk is attached to the rod.

The Attempt at a Solution

I can find the position of the centre of mass of the system, the torque due to gravity and the moment of inertia of the system about the pivot. From this quantities i shall form the equation of motion and thus i can find the time period.

Now i see no reason why the period will change if the disk is free to spin. Firstly i think the disk will not spin since there is no torque acting on it. Both gravity and the force exerted by the rod pass through the bearing. If it also spins the position of centre of mass doesn't change. The moment of inertia of the system too remains unchanged.

Am I correct since I am feeling that I missed something?

 

[TSny]

You are correct that the disk will not rotate if the disk is free to spin.

But, how would you express the disk's angular momentum about the pivot of the pendulum
(a) if the disk rotates with the pendulum?
(b) if the disk does not rotate?

 

[Avi Nandi]

If the spin velocity is constant then the time period will be the same. But if the spin has some acceleration then the oscillation may be damped or lose it's oscillatory character. Am i correct?

 

[TSny]

You have two situations. The first is where the disk and rod form one rigid body so that the disk rotates with the pendulum as the pendulum swings. The second is where the disk does not rotate about its center as the pendulum swings. See picture. The red dot is just a reference mark painted on the disk.