rhemmin
- 4
- 0
Homework Statement
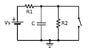
The switch in the circuit is opened at t = 0. Determine the time required for the capacitor to charge to 53% of its maximum voltage in milliseconds. Given that R1 is 8.9 kΩ, R2 is 3.1 kΩ, C is 5.1 μF and Vs is 6 volts. Round your answer off to two decimals.
Homework Equations
i(t)=I(max)*e^(-t/RC) (capacitor current as a function of time)
v(t)=V(max)(1-e^(-t/RC) (capacitor voltage as a function of time)
The Attempt at a Solution
I first determined that the maximum current in the circuit was V/(R1+R2) = 0.5 mA. This would both be the current through the capacitor at t =0+ and the current through the resistors once the capacitor had reached its max charge and acted as a open circuit.
I then determined that the max voltage through the capacitor would equal I(max)*R2(=1.55V) since the capacitor and R2 are in parallel. When the capacitor voltage levels off, it should behave like an open circuit so all of the current should flow through the loop including Vs, R1, and R2.
53% of max capacitor voltage should be .53(1.55) = .8215V.
I then used the capacitor voltage function listed in relevant equations to solve for t.
I'm not sure exactly which resistance value to use for the time constant. I've tried R1, R2, and R1+R2 without success. Could someone help explain
Thanks for the help!