m4r35n357
- 657
- 148
I would appreciate it if some senior member would give me feedback about this result that I have been using in my raytracing simulations of relativistic flight, https://www.youtube.com/playlist?list=PLvGnzGhIWTGR8QYYvMCweXPHtZPnsjrw8.
For simplicity I am assuming that the primed and unprimed coordinate origins concide, and that ##c = 1##.
Starting from the general Lorentz transform in 2+1 spacetime for an observer in the primed frame moving along the ##x## axis at velocity ##v## through a "scene" at rest in the unprimed frame:
$$
\left(\matrix{%
t' \cr
x' \cr
y'
}\right)
=
\left(\matrix{%
\gamma & -v\gamma & 0 \cr
-v\gamma & \gamma & 0 \cr
0 & 0 & 1
}\right)
\left(\matrix{%
t \cr
x \cr
y
}\right)
$$
Which can be used straightforwardly to derive the exresssions for aberration, doppler shift etc. The light travel delay from any point (##x, y##) in the unprimed frame to a stationary observer at the origin is given by the ##t## component, and to a moving observer is given by the ##t'## component. If we apply the light cone constraint (light delay is just the radial distance from the observer to a point,##R = \sqrt(x^2 + y^2)##, similarly for ##R'## in the primed frame) to this we have:
$$
\left(\matrix{%
R' \cr
R' \cos \alpha' \cr
R' \sin \alpha'
}\right)
=
\left(\matrix{%
\gamma & -v\gamma & 0 \cr
-v\gamma & \gamma & 0 \cr
0 & 0 & 1
}\right)
\left(\matrix{%
R \cr
R \cos \alpha \cr
R \sin \alpha
}\right)
=
\left(\matrix{%
\gamma R (1 - v \cos \alpha) \cr
\gamma R (\cos \alpha - v) \cr
R \sin \alpha
}\right)
$$
where ##\frac{y}{x} = \tan \alpha## and ##\frac{y'}{x'} = \tan \alpha'##, so that:
$$
R' = \gamma (1 - v \cos \alpha) R
$$
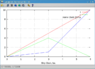
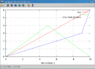
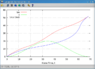
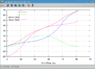
which gives the light travel delay in terms of quantities in the unprimed frame (this is simpler). Note that the ratio of ##R'## to ##R## is numerically identical to the doppler factor. The time ##T## seen on the clock face by the moving observer is then given by subtracting ##R'## from the coordinate time in the unprimed frame:
$$
T = t - \gamma (1 - v \cos \alpha) R = t - \frac{\sqrt(x^2 + y^2) (1 - v \cos \alpha)}{\sqrt(1 - v^2)}
$$
In words; the time on the clock face seen by the moving observer is the coordinate time in the rest frame, delayed in line with the transformed light cone in the observer's frame.
As I said, comments and corrections welcome!
For simplicity I am assuming that the primed and unprimed coordinate origins concide, and that ##c = 1##.
Starting from the general Lorentz transform in 2+1 spacetime for an observer in the primed frame moving along the ##x## axis at velocity ##v## through a "scene" at rest in the unprimed frame:
$$
\left(\matrix{%
t' \cr
x' \cr
y'
}\right)
=
\left(\matrix{%
\gamma & -v\gamma & 0 \cr
-v\gamma & \gamma & 0 \cr
0 & 0 & 1
}\right)
\left(\matrix{%
t \cr
x \cr
y
}\right)
$$
Which can be used straightforwardly to derive the exresssions for aberration, doppler shift etc. The light travel delay from any point (##x, y##) in the unprimed frame to a stationary observer at the origin is given by the ##t## component, and to a moving observer is given by the ##t'## component. If we apply the light cone constraint (light delay is just the radial distance from the observer to a point,##R = \sqrt(x^2 + y^2)##, similarly for ##R'## in the primed frame) to this we have:
$$
\left(\matrix{%
R' \cr
R' \cos \alpha' \cr
R' \sin \alpha'
}\right)
=
\left(\matrix{%
\gamma & -v\gamma & 0 \cr
-v\gamma & \gamma & 0 \cr
0 & 0 & 1
}\right)
\left(\matrix{%
R \cr
R \cos \alpha \cr
R \sin \alpha
}\right)
=
\left(\matrix{%
\gamma R (1 - v \cos \alpha) \cr
\gamma R (\cos \alpha - v) \cr
R \sin \alpha
}\right)
$$
where ##\frac{y}{x} = \tan \alpha## and ##\frac{y'}{x'} = \tan \alpha'##, so that:
$$
R' = \gamma (1 - v \cos \alpha) R
$$
which gives the light travel delay in terms of quantities in the unprimed frame (this is simpler). Note that the ratio of ##R'## to ##R## is numerically identical to the doppler factor. The time ##T## seen on the clock face by the moving observer is then given by subtracting ##R'## from the coordinate time in the unprimed frame:
$$
T = t - \gamma (1 - v \cos \alpha) R = t - \frac{\sqrt(x^2 + y^2) (1 - v \cos \alpha)}{\sqrt(1 - v^2)}
$$
In words; the time on the clock face seen by the moving observer is the coordinate time in the rest frame, delayed in line with the transformed light cone in the observer's frame.
As I said, comments and corrections welcome!
Last edited: