Toothpaste dispenser: friction between rollers

[thijsdb]

Hi there,

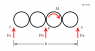
I'm trying to get a grip on this 1930's toothpaste dispenser. The basic idea is that you place a tube in de dispenser between the rollers, and then rotate one of the rollers with the key in order to dispense some toothpaste. Since the gears are connected to the first roller, the other roller also rotates and also the entire carriage moves downwards since two gears are connected to the racks on the side.

My question:

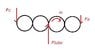
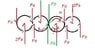
when we have an equilibrium of the whole carriage and we visualize it from the side, 3 forces and one moment are there: 2 forces on the intersection of the two side gears whith the racks (Fa & Fc), the moment (m) about the roller and the resultant force of the tube on the roller. (ALL other forces drawn are internal to the carriage)
Since the moment on the roller is not in the centre, Fa =/= Fc, and so the resultant force of the tube (the two blue ones) is not equal to zero since Fa+Fc+Ftube=0.
But if we assume that the tube itself is just hanging there (which is possible), the tube itself ONLY undergoes the opposite force Ftube, so it can't be in equilibrium!
Since it seems like a possible situation, something in this scenarion isn't right. I hope someone can help!

thanks!

 

[Unrest]

I don't think you're including all the forces that the rollers apply to the tube.

They are probably "stretching" the tube by pulling the top of it upwards (via friction with the rollers) and pushing the bottom of it downwards by the rollers being driven into the wider toothpaste-filled part of the tube. That latter force seems to be the only one you included.

So there could easily be no net force on the tube.

 

[thijsdb]

Hi Unrest,
thanks for your reply. I realize the stretching force is upward and the other one is downwards, so that means 2 forces on each roller (drawn in 1st FBD in a not well chosen direction). But I concluded that the resultant force should be downwards, given the forces on the side gears of 2nd FBD..
So the problem could be in these two forces on the gears, but I can't see it!

 

[Unrest]

If the toothpaste tube is just hanging there then it can't apply any vertical force, as you said. The Fa and Fc on your 2nd diagram are the only vertical forces so they must be equal and opposite.

So Fa would be upwards, not downwards.

Then you just have to follow through the gears to see how those forces get there from the key. I guess however you found that Fa has less magnitude than Fc you could have subtracted even more to make it negative.

I'd ignore the details of how toothpaste tube applies forces to the rollers and just treat it as friction between each roller and the carriage frame.

 

[nvn]

Since the moment on the roller is not in the centre, Fa ≠ Fc.

False. Moment m does not need to be in the centre. Fa equals Fc. And your second attached file is correct.

If, on the other hand, the tube is just hanging, then the direction of all forces in your second attached file would be reversed, and m = 0. And it is in equilibrium.

 

[thijsdb]

"False. Moment m does not need to be in the centre. Fa equals Fc. And your second attached file is correct."

indeed, that was false..
However m cannot be 0 since we assume it not to be ( we try to establish an equilibrium when this moment in applied, i.e. when we don't turn the key hard enough to get the machine working)

Unrest:
Yeah since we concluded the tube won't aply any vertical force, Fb and Fa should be opposite and equal to compensate the moment. In this image I draw this situation, every gear isolated (but positioned next to each other.) We threat the friction as a (small) moments applied against the direction of the roller (and thus the gear).
Fb=Fa, zo i called everything Fa, I use Fb for a new force now
Still there is something wrong!

the 2nd gear from the left is subjected to the moment of the roller, therefor Fb>Fa. Fb acts opposite on the 3rd gear, which is also subjected to Fa: but the difference between the 2nd and the 3rd gear is that the 3rd gear is subjected to two moments

In other words: the fact that we subject only ONE of the rollers to a moment, should cause the rollers to produce a-symetrical moments.

is this correct?

 

[nvn]

Oops. I retract my statement in post 5 where I said Fc equals Fa. I currently agree with the original statement by thijsdb in post 1, that Fc ≠ Fa, when m > 0 (regardless of whether m is in the centre or not). I still agree that the second attached file in post 1 is correct.

I would say, limit the question to only one load case, for now -- the load case when the tube is not just hanging. Assume friction is zero, for now. Then try to solve for the unknowns (Fa, Fb, and Fc). The problem is, there currently appears to be three unknowns, but only two statics equations, unless I am missing something. I have not quite figured that out.

 

[Unrest]

I would say, limit the question to only one load case, for now -- the load case when the tube is not just hanging.

I think we have a terminology problem. When I said "just hanging" I meant it's not being pushed against the bottom of the machine, or otherwise fixed in place. Ie. it's only attached at the rollers. I assumed the weight of the tube was negligible.

In this situation there must be zero net force on the tube in equilibrium.

Is that what you meant too, thij?

 

[nvn]

Unrest: I have the same understanding of "just hanging" as you described in post 8, except I do not assume the tube weight is negligible. Maybe the "just hanging" load case is the main load case thijsdb is asking about in this thread.

 

[thijsdb]

The only assumed load here was the moment placed on one of the rollers, the vertical force Ftube in the 2nd attachement was placed there in order to compensate the two other vertical forces. But since I think the weight of the tube is negligible, the tube won't be in equilibirum, so Ftube must me zero.
I think we can neglect the weight of the tube because we can easily imaging this machine working when flipped on the side.

However what I now think will happen is the following:

I think because of the a-symmetrical forces of the rollers placed on the tube (olny one of them is turned) causes the tube to turn to one side. [imagine th tube being an very streight, stiff piece of wood]. Then a horizontal force will keep the tube in place. > So the nozzle would indeed have to be fixed!

 

[Unrest]

I think because of the a-symmetrical forces of the rollers placed on the tube (olny one of them is turned)

No, the rollers are locked together by the gears, so they're both turned. The tube won't know which one the key is attached to. If it somehow applies more resistance to one roller than the other then that roller's shaft will carry more torque, regardless which one it is.

I think your most recent picture is fine. It also gives balanced forces on the carriage frame. And by balancing moments on the carriage frame you can show that Fa/Fb = 3/5.

 

[thijsdb]

You are right, I thought the 3rd gear was not in equilibrium, but i didn't look properly at the directions of the moments and forces on the 3rd gear.
Naming the small drawn moments 'msmall' We can also conclude that m - msmall = msmall, hence m=2*msmall from the 2nd and 3rd roller.

Thanks so much for your help guys!

 

[nvn]

So we have the following load cases, where mu = coefficient of friction (COF). And in all load cases, tube weight is negligible, W = 0.

• Load case 1: Tube not just hanging, m > 0, mu = 0.
• Load case 2: Tube just hanging, m > 0, mu = 0.
• Load case 3: Same as load case 1, except mu > 0.
• Load case 4: Same as load case 2, except mu > 0.

Unrest: In your last sentence of post 11, are you referring to load case 2?

 

[Unrest]

So we have the following load cases, where mu = coefficient of friction (COF). And in all load cases, tube weight is negligible, W = 0.

• Load case 1: Tube not just hanging, m > 0, mu = 0.
• Load case 2: Tube just hanging, m > 0, mu = 0.
• Load case 3: Same as load case 1, except mu > 0.
• Load case 4: Same as load case 2, except mu > 0.

Unrest: In your last sentence of post 11, are you referring to load case 2?

I don't understand. What's "not just hanging"? What's the coefficient of friction of? The bearings of the shafts? Or the roller's grip on the toothpaste tube? I think we both treated bearings to be frictionless and rollers to be non-slipping.

Hey thij after all this looking at it I want one for my bathroom!

 

[thijsdb]

haha! actually we are developing it for oil paint, since the product is about saving the expensive contents of the tube. oh and it's "thijs" by the way :).
NVN I also don't understand it: right now I can calculate the moment on the roller given the moment on the key. With this I can calculate (given the radius of the roller) the friction needed. Then I can "play" with combinations of material with a certain mu and de force with which the rollers should be pressed against the tube. [pressure and mu gives me fritctional force]

 

[nvn]

Unrest: "Not just hanging" means the toothpaste tube is being pushed against the bottom of the machine. When mu = 0, it means the bearings are frictionless, and the roller friction on the tube is zero. (Even in load case 2, you do not need friction to just hang the tube, because the tube is interlocked on the rollers, due to a slight expansion of the tube after it exits the rollers. However, in load case 2, it is unlikely the tube would feed further into the rollers, because the rollers would probably slip, if mu = 0.)

Which load case were you referring to in your last sentence of post 11?

 

[nvn]

I redrew the diagram (attached) such that positive is upward for all external forces acting on the carriage assembly. Fb is the resultant external force exerted by the tube on the carriage assembly. The distance between the side racks is h; and h = 4*d, where d = gear pitch diameter.

For load case 2, let's say bearing friction is zero, but roller friction is high, such that the rollers do not slip. And as stated earlier, for all load cases, the tube is weightless. Therefore, for load case 2, the solution is Fb = 0, Fa = M/h, and Fc = -M/h.

For load case 1, the solution is,

Fa = -0.5*Fb + (M/h),
Fc = -0.5*Fb - (M/h).​

The problem is, you do not know Fb. I think load case 1 might be statically indeterminate. Perhaps the only way you can determine Fb is to apply a moment M, then measure Fb. After you obtain Fb, then you can compute Fa and Fc.

 

[thijsdb]

Yes indeed load case 1 is statically indeterminate, that is i think the problem stated in the #1.
Load case 2 is the one I drew in my last picture and which Unrest is referring to in #11.

For me this is fine, since the load case 1 only occurs if the roller friction is NOT sufficient and the rollers slip: the carriage then will nonetheless move downwards because of the gears/racks, crushing the tube ..

So what I'm saying is that in case 1: Fb=/=0 ---> tube slips

Because if the tube doesnt slip it gets pulled through with the same speed as the carriadge is moving down*, so the system won't push the tube down --> Fb=0

*an important point I forgot to mention about this system: the size of the rollers and gears are chosen in such way that the tube will stay in place when squeezed, and the carriage will move over it

 

[Unrest]

Which load case were you referring to in your last sentence of post 11?

I think we've only been talking about load case 2 all along. But where mu is only the friction of the bearings and gears, not the rollers.

 

[Unrest]

*an important point I forgot to mention about this system: the size of the rollers and gears are chosen in such way that the tube will stay in place when squeezed, and the carriage will move over it

That seems like the ugliest part of this overdesigned "invention". If you can allow the carriage to climb along the tube by itself then all you have is 2 rollers and two gears, or even no gears at all! If the reaction to the key-turning moment were applied to the carriage frame then it would probably stay straight.

 

[thijsdb]

If you can allow the carriage to climb along the tube by itself then all you have is 2 rollers and two gears, or even no gears at all!

Without the housing you mean? A device you just role over the tube while you can walk around with it..
I agree this is a much more economic (in every sense) solution. also there are even simpeler ways of dispensing a tube, just with a key and a kind of 'hairclip' you put around the tube and then role it. I guess we are the victim of our assignment here :(

One benefit: you'll never have to look for your toothpast/oil paint/any other tube