Mechanics89
- 7
- 0
Hello.
I'm having trouble with determining the dynamics of a rod, when one of the ends has a torque applied to it. I've illustrated it in the figure below:
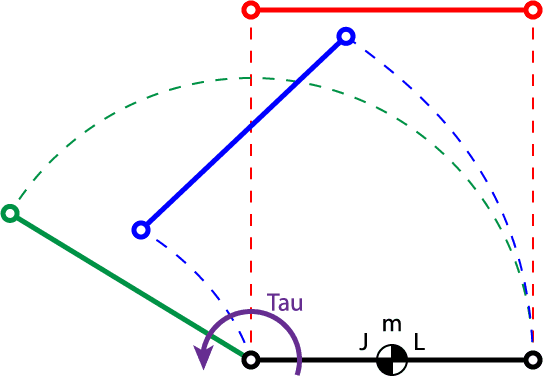
There are no external forces except of the torque - so no gravity, drag etc. Also, the rod is assumed rigid. How will it behave? Green, blue or red? And why?
Legend:
Tau (τ): Torque
m: Mass
J: Moment of inertia
L: Length
I'm having trouble with determining the dynamics of a rod, when one of the ends has a torque applied to it. I've illustrated it in the figure below:
There are no external forces except of the torque - so no gravity, drag etc. Also, the rod is assumed rigid. How will it behave? Green, blue or red? And why?
Legend:
Tau (τ): Torque
m: Mass
J: Moment of inertia
L: Length