Soren4
- 127
- 2
I 'd like to clarify some doubts about the rotational motion around a fixed axis of a rigid body, in the case the angular momentum vector \vec {L} is not parallel to the angular velocity \vec {\omega} .
In particular, consider a horizontal barbell with two equal masses m , forced to rotate around a vertical axis z not passing through the center of the barbell with a constant angular velocity \omega. In this case, considering a point of the axis z for the calculation of momenta (pivot point), \vec {L} , which is the sum of the angular momenta of the two masses, performs a uniform precession motion. Therefore, while the component of \vec{L} parallel to the z axis L_ {z} is constant, its component perpendicular to the axis L_ {n} follows a circular motion with angular velocity \omega .
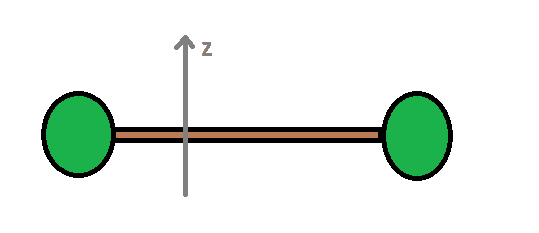
From the theorem of angular momentum, in this case, \vec {\tau} = \frac {d\vec {L}}{dt} \neq 0, so there must be a torque \tau generated by external forces. Since \vec {L} follows a uniform precession motion \vec {\tau} = \frac {d \vec {L}}{dt} = \vec {\omega} \wedge \vec {L} \implies \tau = L_ {n} \omega (1).
My main concern relates to the origin of the torque. The external force in question should be the weight force, which exerts a non zero torque, given the two different distance of the masses from the axis of rotation. However there is also the reaction of the barbell support, which should exert an equal and opposite torque, since the barbell remains in this position during rotation. Now if this is true, then the sum of these two torques is zero, but this can not be given that \vec {L} is varying over time. I can not understand where I'm wrong: maybe I should not consider the reaction of the support?
In addition I would like to ask something about L_ {n} too. This component of \vec {L} in general depends on the pivot point selected for the calculation of the angular momentum, however (in the case of uniform precession) (1) holds. Does this mean that the torque applied by the external forces changes depending on how I choose the pivot for the calculation of \vec {L} ? The torque \vec{\tau} of the external forces calculated with (1) is to be interpreted as the torque with respect to the same pivot used for the calculation of \vec {L} ?
In particular, consider a horizontal barbell with two equal masses m , forced to rotate around a vertical axis z not passing through the center of the barbell with a constant angular velocity \omega. In this case, considering a point of the axis z for the calculation of momenta (pivot point), \vec {L} , which is the sum of the angular momenta of the two masses, performs a uniform precession motion. Therefore, while the component of \vec{L} parallel to the z axis L_ {z} is constant, its component perpendicular to the axis L_ {n} follows a circular motion with angular velocity \omega .
From the theorem of angular momentum, in this case, \vec {\tau} = \frac {d\vec {L}}{dt} \neq 0, so there must be a torque \tau generated by external forces. Since \vec {L} follows a uniform precession motion \vec {\tau} = \frac {d \vec {L}}{dt} = \vec {\omega} \wedge \vec {L} \implies \tau = L_ {n} \omega (1).
My main concern relates to the origin of the torque. The external force in question should be the weight force, which exerts a non zero torque, given the two different distance of the masses from the axis of rotation. However there is also the reaction of the barbell support, which should exert an equal and opposite torque, since the barbell remains in this position during rotation. Now if this is true, then the sum of these two torques is zero, but this can not be given that \vec {L} is varying over time. I can not understand where I'm wrong: maybe I should not consider the reaction of the support?
In addition I would like to ask something about L_ {n} too. This component of \vec {L} in general depends on the pivot point selected for the calculation of the angular momentum, however (in the case of uniform precession) (1) holds. Does this mean that the torque applied by the external forces changes depending on how I choose the pivot for the calculation of \vec {L} ? The torque \vec{\tau} of the external forces calculated with (1) is to be interpreted as the torque with respect to the same pivot used for the calculation of \vec {L} ?