Total Derivatives and Linear Mappings .... D&K Example 2.2.5

[Math Amateur]

I am reading "Multidimensional Real Analysis I: Differentiation" by J. J. Duistermaat and J. A. C. Kolk ...

I am focused on Chapter 2: Differentiation ... ...

I need help with an aspect of Example 2.2.5 ... ...

Duistermaat and Kolk's Example 2.2.5 read as follows:

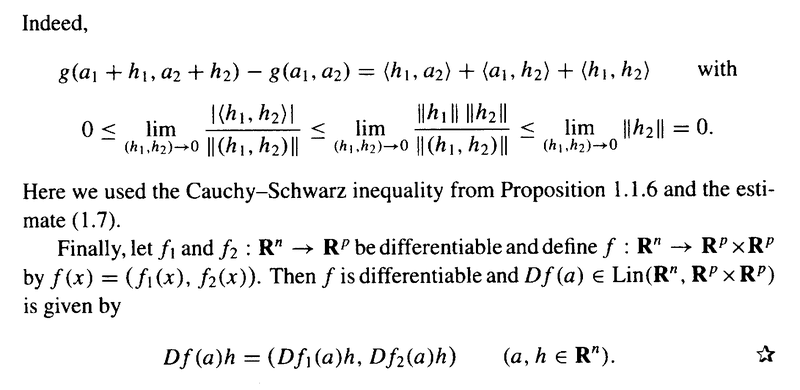In the above text by D&K we read the following:

" ... ... Indeed $A(a+h) - A(a) = A(h)$, for every $h \in \mathbb{R}^n$; and there is no remainder term. ... ... "Now I can see that

$A(a + h) = A(a) + A(h)$ ... ... (1) from the definition of $A$ ...

and in (2.10) we have ...

$A(a +h) - A(a) = DA(a)h + \epsilon_a(h)$ ... ... (2)

So ... from (1) and (2) we get

$A(h) = DA(a)h + \epsilon_a(h)$

... BUT ... why, in D&K's terms is "there no remainder term" ...

... in other words ... why is $\epsilon_a(h) = 0$ ...
Hope someone can help ...

Peter
==========================================================================================***NOTE***

The above post refers to equation (2.10) which occurs in Definition 2.2.2 ... so I am providing Definition 2.2.2 and the accompanying text ... as follows:

I hope that helps readers understand the context and notation of the above post ...

Peter

 

[fresh_42]

If we define $DA(a)(h) := A(h)$ then we get a linear mapping which satisfies the conditions of a derivative and for which the remainder is zero by definition. Now Lemma 2.2.3 says, that there is only one and thus $DA(a)=A$ is the derivative.

 

[andrewkirk]

In the quoted text we have that $DA(a)=A\forall a\in \mathbb R^n$.
hence equation (2) becomes
$$A(a+h)=
A(a)+
DA(a)(h)+\epsilon_a(h)
=A(a)+A(h)+\epsilon_a(h)$$
Subtracting (1) from this gives the desired result.

 

[Math Amateur]

Thanks fresh_42, Andrew ...

... appreciate your help ...

Peter