Total Potential of a Ring at Point P

[Hamiltonian]

Homework Statement

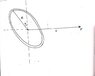
a uniform ring of mass M and radius R is tilted at an angle theta. find the gravitational potential at a point P at a distance r from the center of the ring.

Relevant Equations

gravitational potential = GM/r

I tried finding the potential due to a small element dM of the ring let's say dV, the summation of dV for all the dM's of the ring will give the potential at the point P, but since every element dM of the ring is at a different distance from the point P I am unable to come up with a differential equation to find the potential at P.

 

[anuttarasammyak]

You can take the ring as
x^2+y^2=R^2 or
(x,y,z)=(R \cos\phi,R \sin\phi,0),\ 0<\phi<2\pi
and P
(P_x,P_y,P_z)=(r\sin\theta, 0, r \cos\theta)
Then you can calculate the distance between.

 

[etotheipi]

Is it possible to obtain an algebraic expression? When I set it up, I ended up with an elliptic integral

 

[Hamiltonian]

whats an elliptic integral

 

[etotheipi]

In general an elliptic integral cannot be expressed in terms of elementary functions. The solution I found involved the elliptic integral of the first kind, $F$. I might have made a mistake... so we should wait for a second opinion!

 

[anuttarasammyak]

whats an elliptic integral

Try writing down potential using distance d in post #2 with integration via $\phi$ then you will find it.

 

[Hamiltonian]

You can take the ring as
x^2+y^2=R^2 or
(x,y,z)=(R \cos\phi,R \sin\phi,0),\ 0<\phi<2\pi
and P
(P_x,P_y,P_z)=(r\sin\theta, 0, r \cos\theta)
Then you can calculate the distance between.

here I think you have taken your coordinate system along the ring hence your can write the eq x^2+y^2=R^2
I don't understand how you got
(x,y,z)=(R \cos\phi,R \sin\phi,0),\ 0<\phi<2\pi and what angle phi is over here.

(P_x,P_y,P_z)=(r\sin\theta, 0, r \cos\theta)
if you write the coordinate of point p with origin at the center of the ring and the y-axis along the radii of the ring, how will
Py = 0

 

[haruspex]

and what angle phi is over here.

$\phi$ is the angle around the ring from its intersection with the x-axis to an element of the ring of mass $M\frac{d\phi}{2\pi}$.

 

[haruspex]

Is it possible to obtain an algebraic expression?

The question statement leaves the possibility that an integral expression is acceptable as an answer.

 

[anuttarasammyak]

if you write the coordinate of point p with origin at the center of the ring and the y-axis along the radii of the ring, how will
Py = 0

y axis is chosen so that it is orthogonal to OP.
If we choose x-axis is orthogonal, $P_x=0,P_y=r\sin\theta$ instead.

 

[Hamiltonian]

i am unable to come up with an equation for a tilted circle

 

[etotheipi]

i am unable to come up with an equation for a tilted circle

You don't need to find an equation for the tilted circle; you can just construct a new coordinate system $\mathcal{F'} = \{O; \hat{x}', \hat{y}', \hat{z}'\}$ with the same origin but just rotated so that the ring occupies a plane orthogonal to $\hat{z}'$. Then you can just transform the coordinates of your point P into the new coordinate system (easiest with a diagram). That is what @anuttarasammyak did in #2.

If you really want to find the equation of a tilted circle, you could also try to look at it as the intersection of the sphere $x^2 + y^2 + z^2 = R^2$ and the plane defined by $y=-\tan{(\theta)}x$. Or you could use a coordinate transformation.

 

[anuttarasammyak]

i am unable to come up with an equation for a tilted circle

Instead of a tilted circle and horizontal OP in your figure, in post #2 I take the flat ( or perpendicular ) circle and tilted OP to it by turning them by $-\theta$.

 

[Vitani1]

I did this by introducing an angle phi to represent the angle subtended by the ring. You can use this angle phi and theta to come up with separate expressions for x, y, and z along an axis whose origin is at the bottom of the ring touching the surface. You can use this angle to express the position where you want the potential as some value "x" plus the part of the ring that's has a length in this "x" direction and similarly for y and z. Although I set my coordinate system differently the answers should still work out. Keep in mind this way you have to do an approximation namely that x >>R. Also are you sure you need a differential equation for this? Just use the expression for potential energy and split up M as dM = pdA where p is the density (M/2piR) and dA is the area element (actually you only need a line element) and you can integrate over phi. *Update that is not actually the same as what you did because the potential was calculated at a distance from the base of the ring but this same method will give the correct answer for your problem if the distance is taken from the center of the ring.