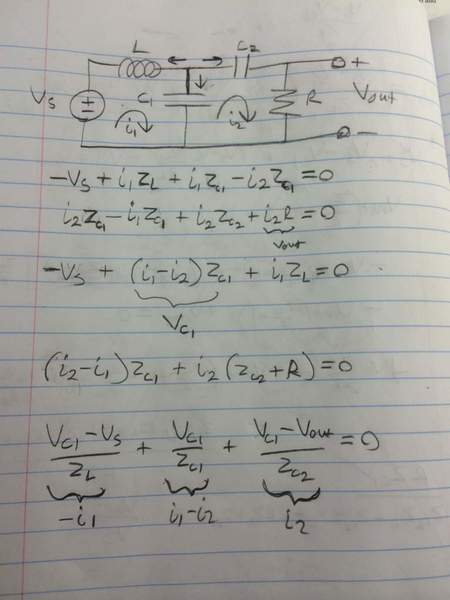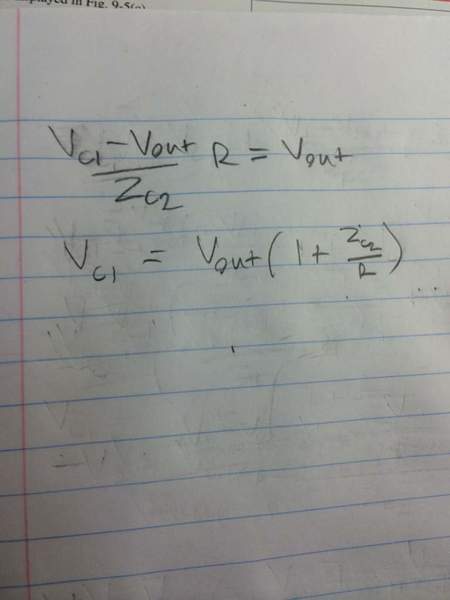Transfer function of third order filter

[gfd43tg]

Hello, I am trying to do this example problem in my textbook

I have my KVL and KCL equations written. I am trying to use substitutions to find V_c1 in terms of Vs and also in terms of Vout, so I can find Vout in terms of Vs. However, it seems like no matter what sequence of substitutions I do yield 0 = 0, and I am not making progress in finding the answer.

 

[gfd43tg]

Here is my closest attempt so far

Edit: I followed through with the algebra and it turns out to give the correct answer. My question though is this: I sort of chose to do this substitution from exhaustion. Meaning, I tried many other substitutions that yielded nothing. In a timed situation, how do I know which substitution I should make so I don't waste time trying other ones that are dead ends?

 

[gfd43tg]

Well, since I got the part with the impedances correct, I am having a hell of a time trying to get it in the form they have with the H(ω). Any tips for this? I am trying to multiply by the complex conjugate but the algebra here is way too much and its too easy to make a mistake.

 

[The Electrician]

You need to make use of this:

Then you can proceed like this:

 

[gfd43tg]

Thanks for that. I will look carefully over these steps.

 

[gfd43tg]

I'm having trouble getting from

''After we make these substitutions...we get these results''

 

[gfd43tg]

I finally got it. That is such an annoying problem. Sometimes I wonder if this is a circuits class or a complex algebra class...

 

[The Electrician]

Sometimes I wonder if this is a circuits class or a complex algebra class...

Count yourself lucky. If it hadn't been for Steinmetz:

http://en.wikipedia.org/wiki/Charles_Proteus_Steinmetz

you would be solving simultaneous differential equations instead of simple algebra with complex arithmetic!