- #1
FrankJ777
- 140
- 6
1. Problem statement
Find the transfer function , H(s) by two methods. Use Nodal analysis with Cramer's method, and decompose into simpler sections and use the property, H(s) = H1(s) * H2(s).
H(s) = H1(s) * H2(s)
H(s) = Vout/Vin
Cramer's Rule. X = Dx/D : where D is the determinant and Dx is the determinate with the x column.[/B]
I used nodal with Cramer's Method, and decomposed into to sections. The transfer functions were similar but the denominators differ by a term, and I don't know why.
First using nodal with Cramer's method. [/B]

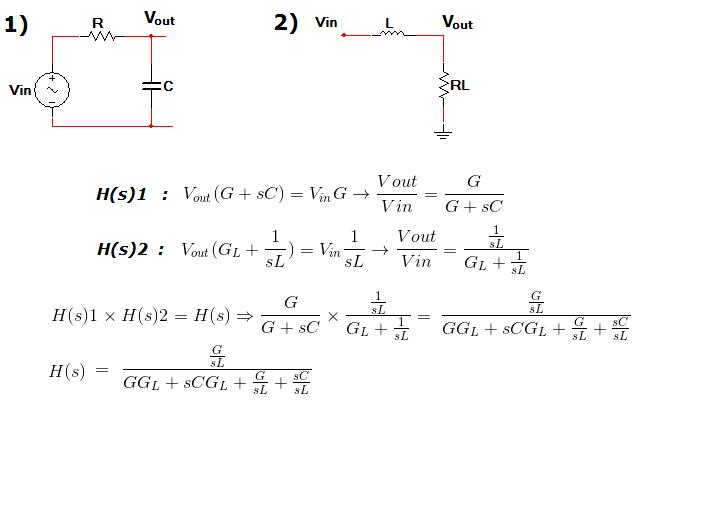
Then decomposing the filter into two filters, finding H(s)1,H(s)2, then H(s)=H(s)1xH(s)2.
Here are the two transfer functions. You can see that they differ by a single term in the denominator, GL/sL circled in red.
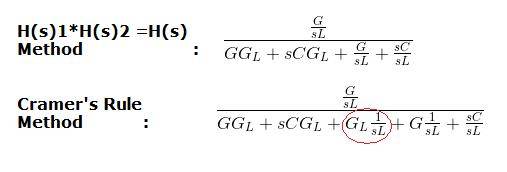
I'm sure they should be the same, but I'm not sure where I'm going wrong. Can anyone point me in the right direction?
Thanks a lot.
Find the transfer function , H(s) by two methods. Use Nodal analysis with Cramer's method, and decompose into simpler sections and use the property, H(s) = H1(s) * H2(s).
Homework Equations
H(s) = H1(s) * H2(s)
H(s) = Vout/Vin
Cramer's Rule. X = Dx/D : where D is the determinant and Dx is the determinate with the x column.[/B]
The Attempt at a Solution
I used nodal with Cramer's Method, and decomposed into to sections. The transfer functions were similar but the denominators differ by a term, and I don't know why.
First using nodal with Cramer's method. [/B]
Then decomposing the filter into two filters, finding H(s)1,H(s)2, then H(s)=H(s)1xH(s)2.
Here are the two transfer functions. You can see that they differ by a single term in the denominator, GL/sL circled in red.
I'm sure they should be the same, but I'm not sure where I'm going wrong. Can anyone point me in the right direction?
Thanks a lot.