Transfer functions of active filters with Amplification

[topcat123]

Homework Statement

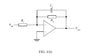
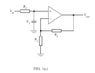
Derive the transfer function for both circuits \frac{V_{out}}{V_{in}} sketch Bode plots for each circuit (amplitude and phase)

Homework Equations

Z_c=\frac{1}{j{\omega}C}~and~{\omega}_C=\frac{1}{RC}

The Attempt at a Solution

We can treat this as a potential divider using the impedances of the resister and caps.
using the Equation for the first circuit (Low pass active)\frac{V_{out}}{V_{in}}=\frac{Z_c}{Z_R+Z_C}Z_R=R
sustituting for Z_C and Z_R

\frac{V_{out}}{V_{in}}=\frac{\frac{1}{j{\omega}C}}{R+\frac{1}{j{\omega}C}}Multiply though by j{\omega}C gives\frac{V_{out}}{V_{in}}=\frac{1}{j{\omega}RC+1}
substituting for RC with w_C
\frac{V_{out}}{V_{in}}=\frac{1}{j\frac{\omega}{\omega_C}+1}

I am not sure how to implement the gain function, I think it is just a case of multiplying by
G=\frac{R_2}{R_1}
as this is negative feed back \frac{V_{out}}{V_{in}}=\frac{-G}{j\frac{\omega}{\omega_C}+1}
Am I on the right lines.
As for the BODE plot when the filter is at cutoff frequance the phase shift will be -45 deg at -3dB with a roll of of 20dB per dec?

All help will be apreciated
Thanks

 

[gneill]

Your method looks okay for the first circuit. You should specify that the R in your ω_C is actually R₂.

Take care with your Bode and phase plots. The 3 dB point will be 3 dB down from the maximum gain (low frequency gain). The phase shift will be 45 degrees from the low frequency phase (and it's a negative gain circuit so near DC the phase shift is...?).

 

[Hesch]

HighJPG:

Z_R2,C1 = Z_R2 || Z_C1 = R₂*(1/sC₁) / (R₂+1/sC₁) = R₂ / (sC₁R₂+1)

Z_R1 = R₁

Vout/Vin = -Z_R2,C1 / Z_R1 = -R2 / ( sC₁R₂R₁ + R₁ )

If you are not familiar with Laplace, just substitute s = jω as for sinusoidal signal ( Bode ).

 

[topcat123]

The phase shift will be 45 degrees from the low frequency phase (and it's a negative gain circuit so near DC the phase shift is...?).

At DC the phase shift is 0 deg 0dB? and w_c -45 deg -180 deg at about -40dB?

 

[gneill]

At DC the phase shift is 0 deg 0dB? and w_c -45 deg -180 deg at about -40dB?

At DC the circuit looks like a standard inverting amplifier. It has a gain set by the resistors R1 and R2:

$\frac{V_{out}}{V_{in}} = - \frac{R_2}{R_1}$

Note carefully the negative sign!

 

[topcat123]

Circuit 2 also a low frequency pass (integrator)
the gain is\frac{V_{out}}{V_{in}}=\frac{-Z}{R_1}
z=\frac{X_CR_2}{X_C+R_2}~~as~~X_C=\frac{1}{j{\omega}C}
Z=\frac{\frac{1}{j{\omega}C}{R_2}} {\frac{1}{j{\omega}C}+{R_2}}
multiplying throgh by jwC.
Z=\frac{R_2}{1+j{\omega}CR_2}
the gain is\frac{V_{out}}{V_{in}}=\frac{-Z}{R_1}=\frac{1}{R_1}*-R_2*\frac{1}{1+j{\omega}CR_2}=\frac{-R_2}{R_1}\frac{1}{1+j{\omega}CR_2}
and as G=\frac{R_2}{R_1}
then \frac{-G}{1+j{\omega}CR_2}
This gives the same first order TF as the circuit before I believe it wil has the same BODE plot too?

As there are no values give how can I sketch a BODE plot for the Gain

VoutVin=−R2R1

 

[gneill]

For the second circuit, I'd find the expression for the DC gain first. The feedback path is divided (R2 and R3), so the gain won't be so simple as a ratio of R2/R1.

A sketch of a bode plot doesn't need to have accurate values. Just label significant features (like the corner frequency) with the appropriate expression from your derivations. That said you can always pick some typical part values and use the result to find the general shape as a basis for your sketch.

 

[topcat123]

For the second circuit, I'd find the expression for the DC gain first. The feedback path is divided (R2 and R3), so the gain won't be so simple as a ratio of R2/R1.

There is no R3 in the second circuit?
I may be getting mixed up somewhere.

Is the TF for the first circuit ok?
Where have I gone wrong with the second?

thanks for all your help
gneill

 

[gneill]

Your second image:

Definitely an R3 in there!

Your first circuit TF work looks okay.

 

[topcat123]

I see the confusion.
fig.1(a) and fig.1(b) the above fig is what i am referring to as the first circuit (fig.1(a)) and the second (fig.1(b))
I should have used the correct idents from the beginning sorry.

So in the DC gain for fig.1(a) should be G=\frac{R_2}{R_3}

I am not sure how to implement the gain function, I think it is just a case of multiplying by

G=R2R1​

This is wrong mabe a typo in post " #1"

and the DC gain for fig.1(b) isG=\frac{R_2}{R_1}

 

[gneill]

I see the confusion.
fig.1(a) and fig.1(b) the above fig is what i am referring to as the first circuit (fig.1(a)) and the second (fig.1(b))
I should have used the correct idents from the beginning sorry.

Ah. Well that's a horse of a different color then

So in the DC gain for fig.1(a) should be G=\frac{R_2}{R_3}

You want to check that. Have you analyzed the circuit? Note that since no current can flow into the op-amp inputs, the junction of the R2~R3 divider must be equal to Vin (essentially no input current so no potential drop across R1).

and the DC gain for fig.1(b) isG=\frac{R_2}{R_1}

The gain should be negative for fig.1(b).