Discussion Overview
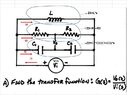
The discussion revolves around analyzing a circuit involving resistors, capacitors, and an inductor, specifically focusing on the output voltage (Vo) and its relationship with the input voltage (Vi). Participants explore various methods for circuit analysis, including Kirchhoff's laws and impedance transformations, while seeking to derive the transfer function.
Discussion Character
- Technical explanation
- Mathematical reasoning
- Debate/contested
Main Points Raised
- One participant expresses confusion about applying Kirchhoff's voltage law in a circuit where Vo is embedded, questioning how to set up the equations correctly.
- Another participant suggests labeling the currents in the diagram to clarify their directions and recommends converting components to impedances for easier analysis.
- A participant acknowledges the feedback and seeks validation of their work, indicating they have modified the circuit to a three-loop configuration but have not yet derived the transfer function.
- One participant provides a mathematical approach involving impedances, suggesting relationships between the input and output voltages through various impedances.
- Another participant advises removing the inductor from consideration, arguing that it does not affect Vo and suggesting a voltage divider approach to calculate Vo based on the resistors and capacitors.
Areas of Agreement / Disagreement
Participants present differing views on the role of the inductor and the best methods for analyzing the circuit. There is no consensus on the correct approach or the final configuration of the circuit, indicating ongoing debate and exploration of ideas.
Contextual Notes
Some assumptions about the circuit configuration and the roles of components remain unverified. The discussion includes various mathematical expressions and transformations that have not been fully resolved or agreed upon.