SUMMARY
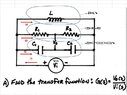
This discussion focuses on analyzing a four-loop circuit using Kirchhoff's voltage law and the node voltage method. The user is attempting to derive the transfer function while dealing with the complexities introduced by the output voltage (Vo) embedded in the circuit. Key equations discussed include I1 = I2 + I3 + I4 and the conversion of circuit components into impedances for easier analysis in the s-domain. The conversation emphasizes the importance of voltage dividers and the relationship between the components to calculate Vo accurately.
PREREQUISITES
- Understanding of Kirchhoff's voltage law
- Familiarity with circuit analysis techniques, specifically node voltage method
- Knowledge of impedance in the s-domain for inductors, capacitors, and resistors
- Ability to apply voltage divider principles in circuit analysis
NEXT STEPS
- Learn how to convert circuit components into impedances in the s-domain
- Study the application of the node voltage method in complex circuits
- Research voltage divider formulas and their applications in circuit analysis
- Explore transfer function derivation techniques for multi-loop circuits
USEFUL FOR
Electrical engineering students, circuit designers, and anyone involved in advanced circuit analysis and design, particularly those working with multi-loop circuits and transfer functions.