Transients(RC) elements in the circuit after commutation?

[builder_user]

Homework Statement

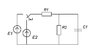
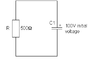
Find I1,I2,I3,Uc

Homework Equations

I was trying to make this task but my result was not correct
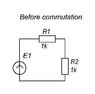
Before commutation
I=E/(R1+R2)=0.1 A
U=0.1*R2=100 V
After commutation
I=0 A
In the moment
equatations
I1*R1+I1*R2-I3*R2=E
I3*R2-I1*R2=Uc

I3=C*dUc/dt

But when I had got result
Uc=-200e^(-100t)+100
It was not correct.

The Attempt at a Solution

R1=1000 Ohms
R2=1000 Ohms
C=20*10^-6 F
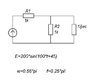
case 1
1)
E1=200 v
E2=0
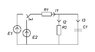
case 2
2)
E1=200 V
E2=200 V
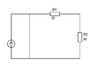
case 3
3)
E1=200sin(100t+45*)
E2=100

Are there any elements in the circuit after commutation?
Currents have Clockwise direction

There won't many changes in case 2.
But is there impendance in case 3?

 

[gneill]

Could you label your diagram with the currents?

Which case are you evaluating? You seem to have an attempt at solution under "Relevant Equations" and additional problem information under "Attempt at a Solution".

 

[builder_user]

Could you label your diagram with the currents?

pic.1?

Which case are you evaluating?

I evaluate first case.all my results are equal to (-1)*results in the keys

 

[gneill]

For the first case, when the switch closes the capacitor will discharge from 100V down to zero volts through the parallel combination of R1 and R2. The first thing to do is to evaluate the time constant (I see that you've calculated its inverse, 100s^-1). Then just write the appropriate equations for exponential decay, Uc(t), Ic(t). The resistor currents can be found using the voltage equation.

 

[builder_user]

parallel combination of R1 and R2.

Why parallel?

 

[gneill]

Why parallel?

Because both ends of R1 and R2 are connected. Wouldn't you call that parallel?

EDIT: I should point out that this happens for case 1 because E2 is defined to be 0V.

 

[builder_user]

Because both ends of R1 and R2 are connected. Wouldn't you call that parallel?

But I can see only one connected end - node with capacitor+R1+R2.

If E2=0 -> there won't branch with E2 correct?

 

[gneill]

But I can see only one connected end - node with capacitor+R1+R2.

If E2=0 -> there won't branch with E2 correct?

E2 = 0 is the same as E2 being replaced with a short circuit (a wire).

 

[builder_user]

E2 = 0 is the same as E2 being replaced with a short circuit (a wire).

Before commutation?

 

[gneill]

Before the switch is moved, Only E1 is connected to the resistor/capacitor network.

 

[builder_user]

So the previous circuit is after?

 

[gneill]

So the previous circuit is after?

Not quite. Immediately after the switch is moved E1 disappears from consideration and the switch connects R1 to ground (via the zero potential of E2). The capacitor should be there, still charged to its pre-switching value of E1/2.

A long time after the switch is moved, then you can say that the capacitor plays no role and effectively disappears.

 

[builder_user]

So I=0 & U=0 after commutation?

U=E1/2 after commutation? But I=0?

 

[gneill]

So I=0 & U=0 after commutation?

A long time after commutation, yes.

Immediately after commutation the capacitor will discharge exponentially through R1 and R2.

 

[gneill]

U=E1/2 after commutation? But I=0?

Immediately after U = E1/2, yes. But it will decay down to zero over time. So the current will be non-zero.

 

[builder_user]

Immediately after U = E1/2, yes. But it will decay down to zero over time. So the current will be non-zero.

But what all does it give?
I will have such equatations in any case
I1*R1+I1*R2-I3*R2=E
I3*R2-I1*R2=U

 

[gneill]

But what all does it give?
I will have such equatations in any case
I1*R1+I1*R2-I3*R2=E
I3*R2-I1*R2=U

There's the capacitor to be concerned with, too. It should figure in your equations if you're going to solve the problem that way. You'll end up with a differential equation.

The simple way is to just realize that there will be an exponential decay of the capacitor voltage, and just write down the well known formula for that.

For your case 1, after the switch is moved the equivalent circuit looks like this:

 

[builder_user]

There's the capacitor to be concerned with, too. It should figure in your equations if you're going to solve the problem that way. You'll end up with a differential equation.

It will be there 'cause I'll use i=Cdu/dt

 

[gneill]

Surely you've solved the equation for this simple circuit before, either as an exercise or as a worked example in your text? You should be able to just write down the voltage and current equations without having to go back to solve the differential equation again. This circuit situation shows up so often that it's important to be able to just write down the solution quickly and move on... it will save an enormous amount of time and effort, especially in exams!

 

[builder_user]

Surely you've solved the equation for this simple circuit before, either as an exercise or as a worked example in your text? You should be able to just write down the voltage and current equations without having to go back to solve the differential equation again. This circuit situation shows up so often that it's important to be able to just write down the solution quickly and move on... it will save an enormous amount of time and effort, especially in exams!

I've already failed my exam...Today. I've not done this task(all my results was with (e^(100t)) - as a result I'll need to pass it again on Thursday.

 

[gneill]

You should state when there is a required solution method to be followed. If you must write and solve the differential equation for the circuit, then we can do so.

Since the circuit simplifies to the one shown in post #17, you should be able to write and solve its differential equation for Uc, then apply that result to the full circuit to find the individual currents.

 

[builder_user]

Since the circuit simplifies to the one shown in post #17, you should be able to write and solve its differential equation for Uc, then apply that result to the full circuit to find the individual currents.

Ok. Math part can be solved by Mathcad.

Skip case 2.

In case 3 is there resistance 1/jwC in the circuit?

 

[gneill]

Ok. Math part can be solved by Mathcad.

Skip case 2.

In case 3 is there resistance 1/jwC in the circuit?

Yes, while the switch is in the E1 position (actually, it's called an impedance rather than a resistance). But when the switch moves to E2, that's a DC supply. In order to find out what the transient response is going to be when the switch is thrown, you'll need to know the actual instantaneous voltage on the capacitor at that instant. In other words, you'll need to know at what time, t, the switch is thrown.

You will have to write an equation for the voltage on the capacitor with respect to time when the circuit is being driven by a sinewave. Plug in the time t when the switch action occurs to find the value.

 

[builder_user]

So I can't do like this

Req1=R2*1/(jwC)/(R2+1/(jwC))
Req2=R1+Req1

I=(Emcos(f)+j*Esin(f))/Req2?

 

[gneill]

Sure. (Assuming f = ωt). That applies before the switch is moved to the DC source. What will be the voltage on the capacitor at the instant the switch is moved?

 

[builder_user]

f it's not wt it's

E=Emsin(wt+f)

 

[gneill]

f it's not wt it's

E=Emsin(wt+f)

Ah. Your f is the phase angle. Okay. Then you still need to plug in t to find the instantaneous voltage on the capacitor when the switch is thrown.

 

[builder_user]

Sure. (Assuming f = ωt). That applies before the switch is moved to the DC source. What will be the voltage on the capacitor at the instant the switch is moved?

I think voltage will be the same as voltage on R2

My instant. voltage on C is = 72+69*jand w is the same as w in E(t) right?

When Xc=1/wC without j?

 

[gneill]

Yes, the voltage will be the same as the voltage on the resistor R2, since it is in parallel with the capacitor. But you must include the impedance of the capacitor when you find that voltage. Also, the voltage you find will be a phasor for the steady-state AC voltage on the capacitor -- not the instantaneous voltage at some particular time t.

I've just done a calculation and I find that the phase shift due to the resistor-capacitor network at the given driving frequency actually happens to "undo" the phase shift of the source voltage! So the result is a pure, unshifted sinewave (no phase angle) on the capacitor. Clever choice of component values!

 

[builder_user]

I've just done a calculation and I find that the phase shift due to the resistor-capacitor network at the given driving frequency actually happens to "undo" the phase shift of the source voltage! So the result is a pure, unshifted sinewave (no phase angle) on the capacitor. Clever choice of component values!

Is my result correct or not?


If it is sineware so I just need to find amplitude?
and U will be
U=Umsin(wt+f)?